Trong mỗi bài tập dưới dây, hãy chọn một phương án cho để được khẳng định đúng.
Bài 98
Giá trị biểu thức log236−log2144 bằng
(A) – 4 ; (B) 4 ;
(C) – 2 ; (D) 2.
Lời giải chi tiết:
log236−log2144=log236144
=log214=log22−2=−2
Chọn (C).
Bài 99
Biết log6√a=2 thì log6a bằng:
(A) 36 ; (B) 108 ;
(C) 6 ; (D) 4.
Lời giải chi tiết:
log6√a=2⇔log6a12=2
⇔12log6a=2⇔log6a=4
Chọn (D)
Bài 100
Tập các số x thỏa mãn log0,4(x−4)+1≥0 là:
(A)(4;+∞) (B)(4;6,5)
(C)(−∞;6,5) (D)[6,5;+∞)
Lời giải chi tiết:
log0,4(x−4)+1≥0⇔log0,4(x−4)≥−1⇔0<x−4≤(0,4)−1=52⇔4<x≤132
Vậy S=(4;6,5].
Chọn (B).
Bài 101
Tập các số x thỏa mãn (23)4x≤(32)2−x là:
(A)(−∞;23] (B)[−23;+∞)
(C)(−∞;25] (D)[25;+∞)
Lời giải chi tiết:
(23)4x≤(32)2−x⇔(32)−4x≤(32)2−x⇔−4x≤2−x⇔−3x≤2⇔x≥−23
Vậy S=[−23;+∞).
Chọn (B).
Bài 102
Giá trị biểu thức 3log0,1102,4 bằng:
(A) 0,8; (B) 7,2;
(C) – 7,2; (D) 72.
Lời giải chi tiết:
3log0,1102,4=3.2,4log0,110
=7,2log11010=−7,2log1010=−7,2.
Chọn (C)
Bài 103
Giá trị biểu thức 0,5log225+log2(1,6) bằng:
(A) 1; (B) 2;
(C) 3; (D) 5.
Lời giải chi tiết:
(0,5)log225+log2(1,6)
=12log225+log2(1,6)
=log22512+log2(1,6)
=log25+log2(1,6)
=log2(5.1,6)=log28=3
Chọn (C)
Bài 104
Giá trị biểu thức log2240log3,752−log215log602+log21 bằng:
(A) 4; (B) 3;
(C) 1; (D) – 8.
Lời giải chi tiết:
log2240log3,752−log215log602+log21=log2240.log23,75−log215.log260+0=log2(15.24).log2154−log215.log2(15.4)=(log215+log224).(log215−log24)−log215.(log215+log24)=(log215+4).(log215−2)−log215.(log215+2)=log2215+2log215−8−log2215−2log215=−8
Chọn (D).
Bài 105
Tập các số x thỏa mãn (35)2x−1≤(35)2−x là:
(A)[3;+∞) (B)(−∞;1]
(C)[1;+∞) (D)(−∞;+∞)
Lời giải chi tiết:
BPT⇔2x−1≥2−x
⇔3x≥3⇔x≥1
Vậy S=[1;+∞).
Chọn (C).
Bài 106
Đối với hàm số f(x)=ecos2x, ta có:
(A)f′(π6)=e√32;(B)f′(π6)−e√32;
(C)f′(π6)=√3e(D)f′(π6)=−√3e
Lời giải chi tiết:
f′(x)=(cos2x)′ecos2x
=(2x)′(−sin2x)ecos2x
=−2sin2xecos2x
f′(π6)=−2sinπ3.ecosπ3
=−√3.e12=−√3e
Chọn (D).
Bài 107
Đối với hàm số y=ln1x+1, ta có:
(A)xy′+1=ey;(B)xy′+1=−ey;
(C)xy′−1=ey;(D)xy′−1=−ey.
Lời giải chi tiết:
y=ln1−ln(x+1)=−ln(x+1)⇒y′=−(x+1)′x+1=−1x+1⇒xy′+1=x.−1x+1+1=−xx+1+1=1x+1
Lại có ey=eln1x+1=1x+1
Vậy xy′+1=ey
Chọn (A).
Bài 108
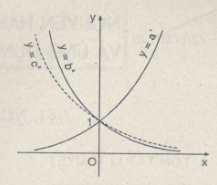
Trên hình bên, đồ thị của ba hàm số: y=ax;y=bx;y=cx (a, b và c là ba số dương khác 1 cho trước) được vẽ trong cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của lũy thừa, hãy so sánh ba số a, b và c.
(A)a>b>c;(B)a>c>b;
(C)b>a>c;(D)b>c>a.
Lời giải chi tiết:
Hàm số y=ax đồng biến trên R nên a>1
Hàm số y=bx,y=cx nghịch biến trên R nên 0<b,c<1
Với x>0 thì bx<cx⇒b<c
Vậy b<c<a
Chọn (B).
Bài 109
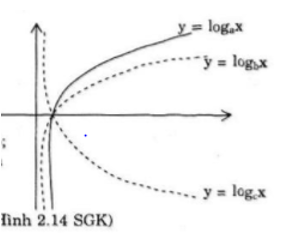
Trên hình bên, đồ thị của ba hàm số: y=logax,logbx,logcx (a,b và c là ba số dương khác 1 cho trước) được vẽ trong cũng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của logarit, hãy so sánh ba số a,b,c:
(A)a>b>c;(B)c>a>b;
(C)b>a>c;(D)c>b>a.
Lời giải chi tiết:
Với x > 0 thì hàm số y= logcx nghịch biến nên 0 < c < 1
Với x > 0 thì hai hàm số y= logax và y=logbx đồng biến nên a > 1; b > 1.
Dựa vào đồ thị với x > 1, ta có logax > logbx nên a < b
Vậy c < a < b.
Chọn (C).
Bài 110
Phương trình log24x−logx22=3 có bao nhiêu nghiệm?
(A) 1 nghiệm (B) 2 nghiệm
(C) 3 nghiệm (D) 4 nghiệm.
Lời giải chi tiết:
Điều kiện: x>0,x≠2
log24x−logx22=3⇔2+log2x−1log2x2=3⇔log2x−1log2x−1=1⇔log22x−log2x−1=log2x−1⇔log22x−2log2x=0⇔[log2x=0log2x=2⇔[x=1x=4
Phương trinh có 2 nghiệm.
Chọn (B).

