LG a
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
f(x)=2x3+3x2+1
Lời giải chi tiết:
Tập xác định: D=R
f′(x)=6x2+6x
f′(x)=0⇔[x=0x=−1
Bảng biến thiên:
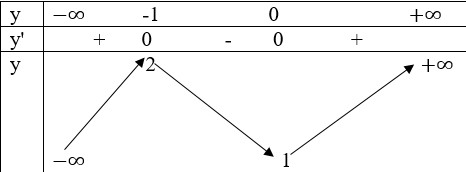
- Hàm số đồng biến trên (−∞;−1) và (0;+∞)
- Hàm số nghịch biến trên (−1;0)
- Hàm số đạt cực tại x=−1;yCĐ=2
- Hàm số đạt cực tiểu tại x=0;yCT=1
lim
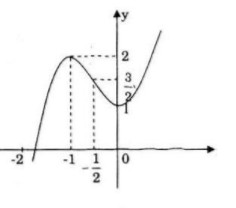
Đồ thị giao trục Oy tại điểm (0;1), đi qua điểm (-1;2).
Điểm uốn:
Ta có y’’ = 12x + 6
y''=0 <=> 12x+6=0
<=> x=-1/2 => y=3/2
LG b
Tìm các giao điểm của đường cong (C) và parabol:
(P):\,\,\,g\left( x \right) = 2{x^2} + 1
Lời giải chi tiết:
Hoành độ giao điểm của đường cong (C) và paraobol (P) là nghiệm của phương trình:
\eqalign{ & \,\,\,\,2{x^3} + 3{x^2} + 1 = 2{x^2} + 1 \cr&\Leftrightarrow 2{x^3} + {x^2} = 0 \cr & \Leftrightarrow {x^2}\left( {2x + 1} \right) = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = - {1 \over 2} \hfill \cr} \right. \cr}
Với x = 0 ta có y = 1; với x = - {1 \over 2} ta có y = {3 \over 2}
Ta có giao điểm A(0;1) và B\left( { - {1 \over 2};{3 \over 2}} \right)
LG c
Viết phương trình các tiếp tuyến của (C) và (P) tại mỗi giao điểm của chúng.
Lời giải chi tiết:
f'\left( x \right) = 6{x^2} + 6x;\,g'\left( x \right) = 4x
f'\left( 0 \right) = 0;\,g'\left( 0 \right) = 0.
Đường thẳng y = 1 là tiếp tuyến chung của (C) và (P) tại điểm A(0;1).
Ta có: f'\left( { - {1 \over 2}} \right) = - {3 \over 2}.
Phương trình tiếp tuyến của (C) tại điểm B là:
y = - {3 \over 2}\left( {x + {1 \over 2}} \right) + {3 \over 2} hay y = - {3 \over 2}x + {3 \over 4}
Lại có: g'\left( { - {1 \over 2}} \right) = - 2.
Phương trình tiếp tuyến của parabol (P) tại điểm B là:
y = - 2\left( {x + {1 \over 2}} \right) + {3 \over 2} hay y = - 2x + {1 \over 2}
LG d
Xác định các khoảng trên đó (C) nằm phía trên hoặc phía dưới (C).
Lời giải chi tiết:
Xét hiệu f\left( x \right) - g\left( x \right)
= 2{x^3} + 3{x^2} + 1 - 2{x^2} - 1
= 2{x^3} + {x^2} = {x^2}\left( {2x + 1} \right)
Xét dấu f\left( x \right) - g\left( x \right):
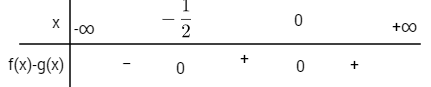
Do đó f\left( x \right) - g\left( x \right) < 0 \Leftrightarrow x < - \frac{1}{2} nên trên khoảng \left( { - \infty ; - {1 \over 2}} \right) thì (C) nằm phía dưới (P)
f\left( x \right) - g\left( x \right) > 0 \Leftrightarrow \left\{ \begin{array}{l} x > - \frac{1}{2}\\ x \ne 0 \end{array} \right. thì f(x) > g(x) hay đồ thị (C) nằm phía trên (P) trên các khoảng \left( { - {1 \over 2};0} \right) và \left( {0; + \infty } \right).

