Đề bài
Với các giá trị nào của a hàm số y=ax−x3 nghịch biến trên R
Phương pháp giải - Xem chi tiết
- Tìm y'.
- Hàm số nghịch biến trên R khi và chỉ khi y'≤0 với mọi x.
Chú ý: Sử dụng định lý về dấu của tam thức bậc hai:
ax2+bx+c≤0(a≠0),∀x∈R ⇔{a<0Δ≤0
Lời giải chi tiết
Cách 1:
Tập xác định D=R
y′=a−3x2
Hàm số nghịch biến trên R ⇔y′≤0,∀x∈R
⇔−3x2+a≤0,∀x∈R⇔{−3<0Δ=02−4.(−3).a≤0⇔12a≤0⇔a≤0
Cách 2. Hàm số nghịch biến trên R, điều kiện y'≤0,∀x ∈R,y'=0 chỉ tại một số hữu hạn điểm.
Ta có: y'≤0 ⇔ a-3x2≤0, ∀x
⇔ 3x2 ≥ a, ∀x ∈R
⇔ a≤min(3x2 ), mà 3x2≥0 ∀x ∈R
Nên min. Vậy a \le 0.
Kết luận: với a≤0 thì y=ax-3x3 nghịch biến trên R.
Cách 3:
Tập xác định D=\mathbb R
y' = a - 3{x^2}
• Nếu a < 0 thì y' < 0 với mọi x \in {\mathbb R}, khi đó hàm số nghịch biến trên \mathbb R.
• Nếu a = 0 thì y' = - 3{x^2} \le 0 với mọi x \in {\mathbb R}, y'=0\Leftrightarrow x=0.
Vậy hàm số nghịch biến trên \mathbb R.
• Nếu a > 0 thì y' = 0 \Leftrightarrow x = \pm {\sqrt {a \over 3}}
Ta có bảng biến thiên
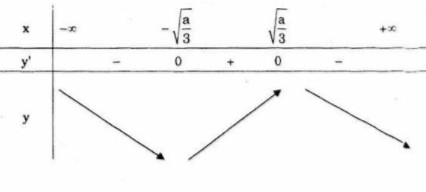
Trong trường hợp này, hàm số không đồng biến trên {\mathbb R}
Vậy hàm số nghịch biến trên {\mathbb R} khi và chỉ khi a \le 0.

