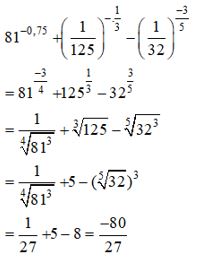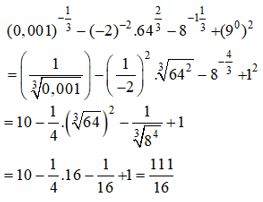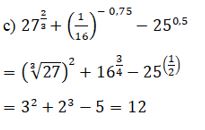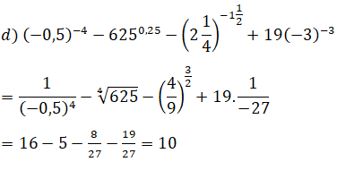Lựa chọn câu để xem lời giải nhanh hơn
Thực hiện phép tính:
a) 81−0,75+(1125)−13−(132)−35;
b) 0,001−13−(−2)−2.6423−8−113 +(90)2;
c) 2723+(116)−0,75−250,5
d) (−0,5)−4−6250,25−(214)−112 +19(−3)−3
LG a
81−0,75+(1125)−13−(132)−35;
Lời giải chi tiết:
81−0,75+(1125)−13−(132)−35
=(34)−34+((15)3)−13−((12)5)−35
=(3)−3+(15)−1−(12)−3
=127+5−8=127−3=−8027
Cách khác:
LG b
0,001−13−(−2)−2.6423−8−113 +(90)2;
Lời giải chi tiết:
0,001−13−(−2)−2.6423−8−113+(90)2
=(10−3)−13−2−2.(26)23−(23)−43+1
=10−22−2−4+1=7−116=11116
Cách khác:
LG c
2723+(116)−0,75−250,5
Lời giải chi tiết:
2723+(116)−0,75−250,5
=(33)23+(2−4)−34−(52)12
=32+23−5=12
Cách khác:
LG d
(−0,5)−4−6250,25−(214)−112 +19(−3)−3
Lời giải chi tiết:
(−0,5)−4−6250,25−(214)−112 +19(−3)−3
=((−2)−1)−4−(54)14−((32)2)−32 +19−27
=24−5−(32)−3−1927
=11−827−1927=10.
Cách khác: