Đề bài
Cho điểm A nằm ngoài mặt cầu S. Chứng minh rằng các đường thẳng đi qua A tiếp xúc với mặt cầu S luôn nằm trên một mặt nón xác định.
Lời giải chi tiết
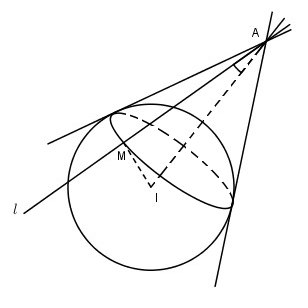
Giả sử Al là một tiếp tuyến của mặt cầu S(I;R) với tiếp điểm là M.
Khi đó nếu Δ là đường thẳng AI và α là góc giữa đường thẳng Al và Δ thì α=^MAI.
Ta có: sinα=MIIA=RIA, suy ra góc α không đổi.
Vậy Al là đường sinh của mặt nón (N) có đỉnh A và góc ở đỉnh là 2α.

