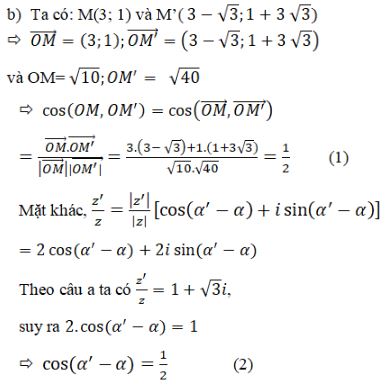Gọi M, M’ là các điểm trong mặt phẳng phức theo thứ tự biểu diễn các số \(z = 3 + i;\) \(z' = \left( {3 - \sqrt 3 } \right) + \left( {1 + 3\sqrt 3 } \right)i.\)
LG a
Tính \({{z'} \over z};\)
Phương pháp giải:
Sử dụng công thức chia hai số phức:
\(\dfrac{{a + bi}}{{c + di}} = \dfrac{{\left( {a + bi} \right)\left( {c - di} \right)}}{{{c^2} + {d^2}}}\)
Lời giải chi tiết:
\(\frac{{z'}}{z} = \frac{{3 - \sqrt 3 + \left( {1 + 3\sqrt 3 } \right)i}}{{3 + i}}\) \(= {{\left[ {3 - \sqrt 3 + \left( {1 + 3\sqrt 3 } \right)i} \right]\left( {3 - i} \right)} \over {3^2+1^2}}\) \( = \frac{{9 - 3\sqrt 3 + 1 + 3\sqrt 3 + \left( {3 + 9\sqrt 3 - 3 + \sqrt 3 } \right)i}}{{10}} \) \(= \frac{{10 + 10\sqrt 3 i}}{{10}}\) \( = 1 + \sqrt 3 i\)
LG b
Chứng minh rằng hiệu số acgumen của z’ với acgumen của z là một số đo của góc lượng giác \(\left( {OM,OM'} \right)\). Tính số đo đó.
Phương pháp giải:
Dựng hình, suy ra kết luận từ hình vẽ.
Lời giải chi tiết:
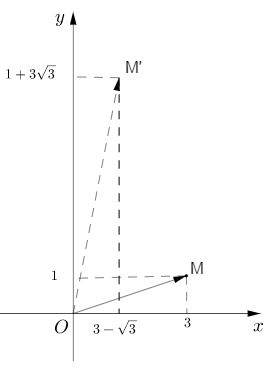
Xét tia Ox thì ta có: \(sđ\left( {OM,OM'} \right) \) \(= sđ\left( {Ox,OM'} \right) - sđ\left( {Ox,OM} \right)\) \( = \varphi ' - \varphi = acgumen{{z'} \over z}\) (sai khác \(k2\pi \))
(trong đó \(\varphi \) và \(\varphi '\) theo thứ tự là acgumen của z và z’).
Từ đó do \({{z'} \over z} = 1 + \sqrt 3 i\) có acgumen là \({\pi \over 3} + k2\pi \,\,\left( {k \in Z} \right)\), nên góc lượng giác \(\left( {OM,OM'} \right)\) có số đo \({\pi \over 3} + k2\pi \,\,\left( {k \in\mathbb Z} \right)\)
Cách khác:
Từ (1) và (2) ta có:
cos(α'-α)=cos(OM,OM')
nên kí hiệu α'-α là một số đo của góc lượng giác (OM, OM’) và số đo là \(\alpha ' - \alpha = \frac{\pi }{3} + k2\pi \).