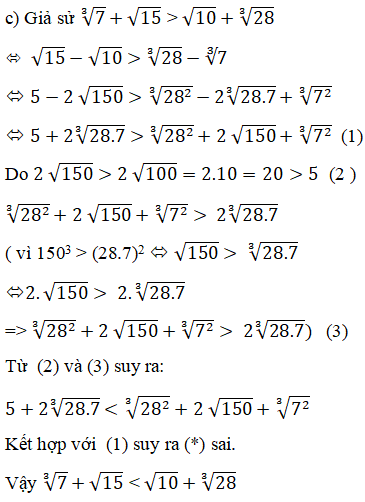So sánh các số
LG a
\(\sqrt 2 \) và \(\root 3 \of 3 \)
Phương pháp giải:
Lũy thừa bậc 6 hai số và so sánh.
Lời giải chi tiết:
Ta có \({\left( {\sqrt 2 } \right)^6} = {2^3} = 8\); \({\left( {\root 3 \of 3 } \right)^6} = {3^2} = 9\)
Do 8 < 9 nên ta có \({\left( {\sqrt 2 } \right)^6}\) < \({\left( {\root 3 \of 3 } \right)^6}\), suy ra \(\sqrt 2 \) < \(\root 3 \of 3 \).
Cách khác:
Giả sử √2 < ∛3 <=> (√2)2 < 3
<=> 2 √2 < 3 <=> 8 < 9 đúng.
Vậy √2 < ∛3
LG b
\(\sqrt 3 + \root 3 \of {30} \) và \(\root 3 \of {63} \)
Phương pháp giải:
So sánh bắc cầu với 4.
Lời giải chi tiết:
\(\sqrt 3 + \root 3 \of {30} > 1 + \root 3 \of {27} = 4 \)
\( \root 3 \of {63} < \root 3 \of {64} =4 \)
Do đó \(\sqrt 3 + \root 3 \of {30} \) > 4 > \(\root 3 \of {63} \).
Vậy \(\sqrt 3 + \root 3 \of {30} \) > \(\root 3 \of {63} \).
Cách khác:
Giả sử √3+∛30 < ∛63
<=> 3√3 + 9∛30 + 3√3∛(302) + 30 < 63
<=> 3 √3 + 9∛3 + 3√3∛(302) < 33 (*)
Ta có 3√3 > 3
9∛30 > 9∛27=27
3√3∛(302) > 3 ∛(27.27) = 27
=> 3√3 + 9∛30 + 3√3∛(302) > 3 + 27 + 27 > 33
Vậy (*) sai => √3+∛30 > ∛63
LG c
\(\root 3 \of 7 + \sqrt {15} \) và \(\sqrt {10} + \root 3 \of {28} \)
Phương pháp giải:
So sánh bắc cầu với 6.
Lời giải chi tiết:
\(\root 3 \of 7 + \sqrt {15} <\sqrt[3]{8} + \sqrt {16} = 2 + 4 =6\)
\(\sqrt {10} + \sqrt[3]{{28}} > \sqrt 9 + \sqrt[3]{{27}} = 3 + 3 = 6\)
Do đó \(\root 3 \of 7 + \sqrt {15} \) < 6 < \(\sqrt {10} + \root 3 \of {28} \)
Vậy \(\root 3 \of 7 + \sqrt {15} \) < \(\sqrt {10} + \root 3 \of {28} \)
Cách khác: