LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số: y=2x2−x+1x−1
Lời giải chi tiết:
Tập xác định: D=R∖{1}
Sự biến thiên:
y′=(4x−1)(x−1)−(2x2−x+1)(x−1)2=2x2−4x(x−1)2y′=0⇔2x2−4x=0⇔2x(x−2)=0⇔[x=0x=2
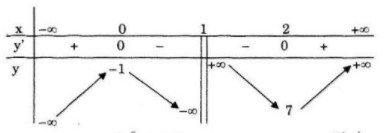
Hàm số đồng biến trên khoảng (−∞;0) và (2;+∞)
Hàm số nghịch biến trên khoảng (0;1) và (1;2)
Cực trị
Hàm số đạt cực đại tại x=0, yCĐ=1
Hàm số đạt cực tiểu tại x=2, yCT=7
Giới hạn:
lim
Tiệm cận đứng là: x=1
\eqalign{ & a = \mathop {\lim }\limits_{x \to \infty } {y \over x} = \mathop {\lim }\limits_{x \to \infty } {{2{x^2} - x + 1} \over {{x^2} - x}} = 2 \cr & b = \mathop {\lim }\limits_{x \to \infty } (y - 2x) \cr&= \mathop {\lim }\limits_{x \to \infty } \left( {{{2{x^2} - x + 1} \over {x - 1}} - 2x} \right) = 1 \cr}
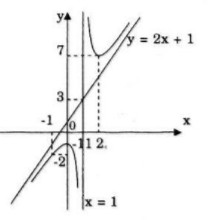
Tiệm cận xiên là: y=2x+1
Bảng biến thiên:
Đồ thị cắt Oy tại điểm (0;-1)
LG b
Với các giá trị nào của m đường thẳng y = m – x cắt đồ thị hàm số đã cho tại hai điểm phân biệt?
Lời giải chi tiết:
Hoành độ giao điểm của đường thẳng và đường cong đã cho là nghiệm của phương trình
\eqalign{ & {{2{x^2} - x + 1} \over {x - 1}} = m - 1\cr& \Rightarrow 2{x^2} - x + 1 = \left( {x - 1} \right)\left( {m - x} \right) \cr & \Leftrightarrow 2{x^2} - x + 1 = - {x^2} + \left( {m + 1} \right)x - m\cr& \Leftrightarrow 3{x^2} - \left( {m + 2} \right)x + m + 1 = 0\,\,\left( 1 \right) \cr}
Đường thẳng cắt đường cong tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 1
\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} \Delta > 0\\ f\left( 1 \right) \ne 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} {\left( {m + 2} \right)^2} - 12\left( {m + 1} \right) > 0\\ {3.1^2} - \left( {m + 2} \right).1 + m + 1 \ne 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} {m^2} - 8m - 8 > 0\\ 2 \ne 0\left( {\text{đúng}} \right) \end{array} \right. \end{array}
\Leftrightarrow m < 4 - 2\sqrt 6 \,\,\text{hoặc}\,\,m > 4 + 2\sqrt {6\,\,} \,\left( 2 \right)
LG c
Gọi A và B là hai giao điểm đó. Tìm tập hợp các trung điểm của đoạn thẳng AB khi m biến thiên.
Lời giải chi tiết:
Hoành độ giao điểm A, B là các nghiệm của (1)
Hoành độ trung điểm M của AB là: {x_M} = {1 \over 2}\left( {{x_A} + {x_B}} \right) = {{m + 2} \over 6}
Vì M nằm trên đường thẳng y = m – x nên {y_M} = m - {x_M} = m - {{m + 2} \over 6} = {{5m - 2} \over 6}
Khử m từ hệ
\left\{ \matrix{ {x_M} = {{m + 2} \over 6} \hfill \cr {y_M} = {{5m - 2} \over 6} \hfill \cr} \right. ta có:
\begin{array}{l} \left\{ \begin{array}{l} 6{x_M} = m + 2\\ 6{y_M} = 5m - 2 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m = 6{x_M} - 2\\ 6{y_M} = 5.\left( {6{x_M} - 2} \right) - 2 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m = 6{x_M} - 2\\ 6{y_M} = 30{x_M} - 12 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m = 6{x_M} - 2\\ {y_M} = 5{x_M} - 2 \end{array} \right. \end{array}
Vậy M nằm trên đường thẳng y = 5x -2
Vì m chỉ lấy giá trị thỏa mãn (2) nên:
m < 4 - 2\sqrt 6 \Rightarrow m = 6{x_M} - 2 < 4 - 2\sqrt 6 \Leftrightarrow 6{x_M} < 6 - 2\sqrt 6 \Rightarrow {x_M} < 1 - {{\sqrt 6 } \over 3}
m > 4 + 2\sqrt 6 \Rightarrow m = 6{x_M} - 2 > 4 + 2\sqrt 6 \Leftrightarrow 6{x_M} > 6 + 2\sqrt 6 \Rightarrow {x_M} > 1 + {{\sqrt 6 } \over 3}
Vậy tập hợp các trung điểm M của đoạn AB là phần của đường thẳng y = 5x -2 với {x_M} < 1 - {{\sqrt 6 } \over 3} hoặc {x_M} > 1 + {{\sqrt 6 } \over 3}

