Tìm cực trị của các hàm số sau:
LG a
\(y = x\sqrt {4 - {x^2}} \)
Lời giải chi tiết:
Tập xác định: \(D = \left[ { - 2;2} \right]\)
\(y' = \sqrt {4 - {x^2}} + x.{{ - x} \over {\sqrt {4 - {x^2}} }} \) \(= {{4 - {x^2} - {x^2}} \over {\sqrt {4 - {x^2}} }} = {{4 - 2{x^2}} \over {\sqrt {4 - {x^2}} }}\)
\(y' = 0 \Leftrightarrow 4 - 2{x^2} = 0 \Leftrightarrow x = \pm \sqrt 2 \)
\(y\left( { - \sqrt 2 } \right) = - 2;y\left( {\sqrt 2 } \right) = 2\)
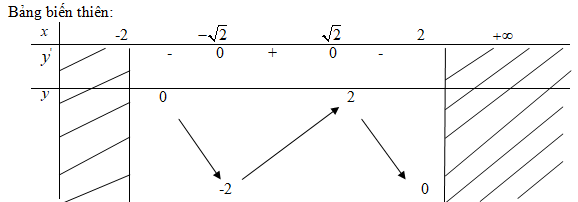
Hàm số đạt cực tiểu tại điểm \(x = - \sqrt 2 \); giá trị cực tiểu \(y\left( { - \sqrt 2 } \right) = - 2\)
Hàm số đạt cực đại tại điểm \(x = \sqrt 2 \); giá trị cực đại \(y\left( {\sqrt 2 } \right) = 2\)
LG b
\(y = \sqrt {8 - {x^2}} \)
Lời giải chi tiết:
TXĐ: \(D = \left[ { - 2\sqrt 2 ;2\sqrt 2 } \right]\)
\(y' = \frac{{\left( {8 - {x^2}} \right)'}}{{2\sqrt {8 - {x^2}} }} = \frac{{ - 2x}}{{2\sqrt {8 - {x^2}} }}= {{ - x} \over {\sqrt {8 - {x^2}} }}\)
\(y' = 0 \Leftrightarrow x = 0\)
\(y\left( 0 \right) = 2\sqrt 2 \)
Bảng biến thiên:
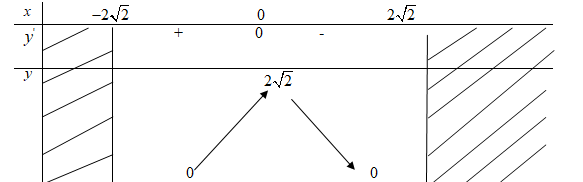
Hàm số đạt cực đại tại điểm \(x=0\), giá trị cực đại \(y\left( 0 \right) = 2\sqrt 2 \)
LG c
\(y = x - \sin 2x + 2\)
Lời giải chi tiết:
Áp dụng quy tắc 2.
TXĐ: \(D=\mathbb R\)
\(\,y' = 1 - 2\cos 2x\)
\(y' = 0 \Leftrightarrow \cos 2x = {1 \over 2} = \cos {\pi \over 3}\)
\(\Leftrightarrow x = \pm {\pi \over 6} + k\pi ,k \in {\mathbb {Z}}\)
\(y'' = 4\sin 2x\)
* Ta có: \(y''\left( {-{\pi \over 6} + k\pi } \right) = 4\sin \left( { - \frac{\pi }{3} + k2\pi } \right)\) \(= 4\sin \left( { - {\pi \over 3}} \right) = - 2\sqrt 3 < 0\)
Do đó hàm số đạt cực đại tại các điểm \(x = - {\pi \over 6} + k\pi ,k \in {\mathbb{Z}}\)
Giá trị cực đại
\(y\left( { - {\pi \over 6} + k\pi } \right) = - {\pi \over 6} + k\pi + {{\sqrt 3 } \over 2} + 2\)
\(y''\left( {{\pi \over 6} + k\pi } \right) = 4\sin \left( { \frac{\pi }{3} + k2\pi } \right)\) \(= 4\sin \left( {{\pi \over 3}} \right) = 2\sqrt 3 > 0\).
Do đó hàm số đạt cực tiểu tại các điểm \(x = {\pi \over 6} + k\pi ,k \in {\mathbb{Z}}\)
Giá trị cực tiểu:
\(y\left( {{\pi \over 6} + k\pi } \right) = {\pi \over 6} + k\pi - {{\sqrt 3 } \over 2} + 2\)
LG d
\(y = 3 - 2\cos x - \cos 2x\)
Lời giải chi tiết:
Áp dụng quy tắc 2.
\(y' = 2\sin x + 2\sin 2x \) \( = 2\sin x + 2.2\sin x\cos x\) \(= 2\sin x\left( {1 + 2\cos x} \right);\)
\(y' = 0 \Leftrightarrow \left[ \matrix{
\sin x = 0 \hfill \cr
\cos x = - {1 \over 2} \hfill \cr} \right. \)
\(\Leftrightarrow \left[ \matrix{
x = k\pi \hfill \cr
x = \pm {{2\pi } \over 3} + 2k\pi ,k \in {\mathbb{Z}} \hfill \cr} \right.\)
\(y'' = \left( {2\sin x + 2\sin 2x} \right)'\) \(= 2\cos x + 4\cos 2x.\)
\(y''\left( {k\pi } \right) = 2\cos k\pi + 4\cos 2k\pi \) \(= 2\cos k\pi + 4 > 0\) với mọi \(k \in {\mathbb{Z}}\)
Do đó hàm số đã cho đạt cực tiểu tại các điểm \(x = k\pi \), giá trị cực tiểu:
\(y\left( {k\pi } \right) = 3 - 2\cos k\pi - \cos 2k\pi \) \(= 2 - 2\cos k\pi \)
\(y''\left( { \pm {{2\pi } \over 3} + k2\pi } \right) \) \(= 2\cos \left( { \pm \frac{{2\pi }}{3} + k2\pi } \right) \) \(+ 4\cos \left( { \pm \frac{{4\pi }}{3} + k4\pi } \right) \) \(= 2.\left( { - \frac{1}{2}} \right) + 4.\left( { - \frac{1}{2}} \right) = - 3 < 0.\)
Do đó hàm số đã cho đạt cực đại tại các điểm \(x = \pm {{2\pi } \over 3} + k2\pi ,k \in {\mathbb{Z}}\); giá trị cực đại:
\(y\left( { \pm {{2\pi } \over 3} + k2\pi } \right) \) \(= 3 - 2\cos {{2\pi } \over 3} - \cos {{4\pi } \over 3} = {9 \over 2}\).
