Tính các tích phân sau :
LG a
π4∫0xcos2xdx;
Phương pháp giải:
Sử dụng phương pháp từng phần {u=xdv=cos2xdx
Lời giải chi tiết:
Đặt
{u=xdv=cos2xdx⇒{du=dxv=12sin2x
Do đó π4∫0xcos2xdx =12xsin2x|π40−12π4∫0sin2xdx
=π8+14cos2x|π40 =π8+14(−1)=π8−14.
LG b
1∫0ln(2−x)2−xdx;
Phương pháp giải:
Sử dụng phương pháp đổi biến u=ln(2−x)
Lời giải chi tiết:
Đặt u=ln(2−x)⇒du=−12−xdx
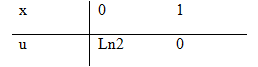
1∫0ln(2−x)2−xdx=−0∫ln2udu=ln2∫0udu =u22|ln20=12(ln2)2
LG c
π2∫0x2cosxdx;
Phương pháp giải:
Sử dụng phương pháp từng phần {u=x2dv=cosxdx
Lời giải chi tiết:
Đặt
{u=x2dv=cosxdx⇒{du=2xdxv=sinx
Do đó I=π2∫0x2cosxdx =x2sinx|π20−2π2∫0xsinxdx =π24−2I1
Với I1=π2∫0xsinxdx
Đặt
{u=xdv=sinxdx⇒{du=dxv=−cosx
Do đó I1=−xcosx|π20+π2∫0cosxdx
=−π2cosπ2+0cos0+sinx|π20 =0+sinπ2−sin0=1
Vậy I=π24−2
LG d
1∫0x2√x3+1dx;
Phương pháp giải:
Đổi biến u=√x3+1
Lời giải chi tiết:
Đặt u=√x3+1⇒u2=x3+1 ⇒2udu=3x2dx⇒x2dx=23udu
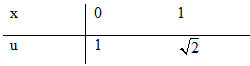
1∫0x2√x3+1dx=23√2∫1u2du=2u39|√21 =29(2√2−1)
LG e
e∫1x2lnxdx.
Phương pháp giải:
Sử dụng phương pháp từng phần {u=lnxdv=x2dx
Lời giải chi tiết:
Đặt
{u=lnxdv=x2dx⇒{du=dxxv=x33
Do đó e∫1x2lnxdx=x33lnx|e1−13e∫1x2dx =e33−19x3|e1=e33−19(e3−1) =2e3+19

