Lựa chọn câu để xem lời giải nhanh hơn
Tính
LG a
π∫05(5−4cost)14sintdt;
Lời giải chi tiết:
Đặt u=5−4cost⇒du=4sintdt ⇒sintdt=14du
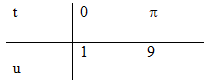
π∫05(5−4cost)14sintdt =54.u14+114+1|91 =549∫1u14du=u54|91=954−1
LG b
√3∫0x3dx√x2+1.
Lời giải chi tiết:
Đặt u=√x2+1⇒u2=x2+1 ⇒udu=xdx ⇒x3dx=x2.xdx=(u2−1)udu
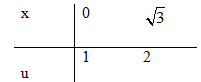
√3∫0x3dx√x2+1=2∫1(u2−1)uudu
2∫1(u2−1)du=(u33−u)|21 =83−2−13+1 =43

