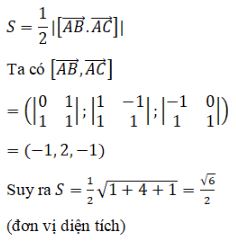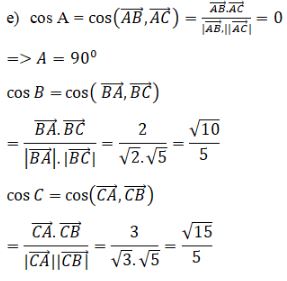Cho ba điểm \(A\left( {1;0;0} \right)\,;\,B\left( {0;0;1} \right)\,;\,C\left( {2;1;1} \right)\)
LG a
Chứng minh A, B, C không thẳng hàng.
Phương pháp giải:
Kiểm tra \( \overrightarrow {BA} ,\overrightarrow {BC} \) không cùng phương.
Lời giải chi tiết:
Ta có \(\overrightarrow {BA} = \left( {1;0; - 1} \right),\overrightarrow {BC} = \left( {2;1;0} \right)\).
Vì \({1 \over 2} \ne {0 \over 1} \Rightarrow \overrightarrow {BA} ,\overrightarrow {BC} \) không cùng phương do đó A, B, C không thẳng hàng.
LG b
Tính chu vi và diện tích tam giác ABC.
Phương pháp giải:
- Tính độ dài các đoạn thẳng AB, BC, CA suy ra chu vi.
- Chứng minh tam giác ABC vuông suy ra diện tích.
Lời giải chi tiết:
Ta có
\(\eqalign{
& AB = \sqrt {{1^2} + {0^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 \cr
& BC = \sqrt {{2^2} + {1^2} + {0^2}} = \sqrt 5 \cr
& AC = \sqrt {{1^2} + {1^2} + {1^2}} = \sqrt 3 \cr} \)
Vậy chu vi tam giác ABC bằng \(\sqrt 2 + \sqrt 3 + \sqrt 5 \).
Ta có \(B{C^2} = A{B^2} + A{C^2} \Rightarrow \Delta ABC \) vuông tại A nên có diện tích \(S = {1 \over 2}AB.AC = {{\sqrt 6 } \over 2}\)
Chú ý:
Có thể tính diện tích theo công thức như sau:
LG c
Tính độ dài đường cao của tam giác ABC kẻ từ đỉnh A.
Phương pháp giải:
Tính chiều cao theo công thức \({h_a} = \frac{{2S}}{a}\)
Lời giải chi tiết:
Gọi \({h_a}\) là độ dài đường cao kẻ từ A ta có:
\({S_{ABC}} = {1 \over 2}BC.{h_a} \) \(\Rightarrow {h_a} = {{2{S_{ABC}}} \over {BC}} = {{\sqrt 6 } \over {\sqrt 5 }} = {{\sqrt {30} } \over 5}\)
LG d
Tính các góc của tam giác ABC.
Lời giải chi tiết:
Vì tam giác ABC vuông tại A nên:
\(\cos B = {{AB} \over {BC}} = {{\sqrt 2 } \over {\sqrt 5 }} = {{\sqrt {10} } \over 5}\)
\(\cos C = {{AC} \over {BC}} = {{\sqrt 3 } \over {\sqrt 5 }} = {{\sqrt {15} } \over 5}\)
Chú ý:
Có thể tính cosB, cosC theo công thức: