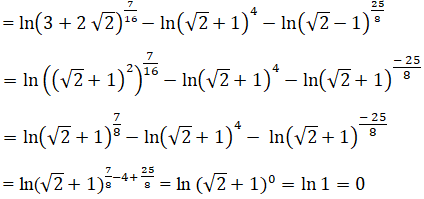Đề bài
Chứng minh:
716ln(3+2√2)−4ln(√2+1)−258ln(√2−1)=0
Lời giải chi tiết
Ta có:
3+2√2=2+2√2+1=(√2)2+2√2+12=(√2+1)2(√2−1)(√2+1)=2−1=1⇒√2−1=1√2+1=(√2+1)−1
Do đó,
716ln(3+2√2)−4ln(√2+1)−258ln(√2−1)
=716ln(√2+1)2−4ln(√2+1)−258ln(√2+1)−1
=716.2ln(√2+1)−4ln(√2+1)−258.(−ln(√2+1))
=78ln(√2+1)−4ln(√2+1)+258ln(√2+1)=0
Cách trình bày khác: