Tìm cực trị của các hàm số sau:
LG a
f(x)=13x3+2x2+3x−1;
Lời giải chi tiết:
TXĐ: D=R
f′(x)=x2+4x+3
f′(x)=0⇔[x=−1x=−3;
f(−1)=−73;f(−3)=−1
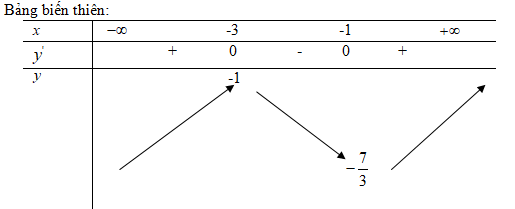
Hàm số đạt cực đại tại điểm x=−3, giá trị cực đại của hàm số là f(−3)=−1
Hàm số đạt cực tiểu tại điểm x=−1, giá trị cực tiểu của hàm số là f(−1)=−73
Cách 2.
f′(x)=x2+4x+3
f′(x)=0⇔[x=−1x=−3;
f’’(x) = 2x + 4
⇒ f’’(-3) = -2 < 0; f’’(-1) = 2 > 0
Vậy hàm đạt cực đại tại điểm x = -3 giá trị cực đại của hàm số là fCĐ = f(-3) = -1.
Hàm số đạt cực tiểu tại điểm x = -1, fCT = f(-1) = -7/3
LG b
f(x)=13x3−x2+2x−10
Lời giải chi tiết:
TXĐ: D=R
f′(x)=x2−2x+2 =(x−1)2+1>0 với mọi x∈R
Hàm số đồng biến trên R, không có cực trị.
LG c
f(x)=x+1x;
Lời giải chi tiết:
TXĐ: D=R∖{0}
f′(x)=1−1x2=x2−1x2;
f′(x)=0⇔[x=1;f(1)=2x=−1;f(−1)=−2
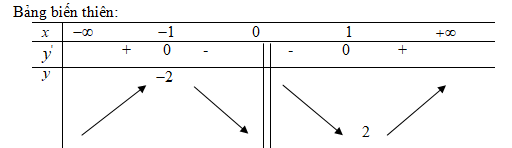
Hàm số đạt cực đại tại điểm x=−1, giá trị cực đại f(−1)=−2. Hàm số đạt cực tiểu tại điểm x=1, giá trị cực tiểu f(1)=2.
Cách khác:
f″ = - \frac{{ - \left( {{x^2}} \right)'}}{{{{\left( {{x^2}} \right)}^2}}} = - \frac{{ - 2x}}{{{x^4}}} = \frac{2}{{{x^3}}}
Vì f’’(- 1) = -2 < 0 nên hàm số đạt cực đại tại x = -1; fCĐ = f(-1) = -2
f'' (1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1; fCT = f(1) = 2.
LG d
f\left( x \right) = \left| x \right|\left( {x + 2} \right);
Lời giải chi tiết:
TXĐ: D=\mathbb R
Hàm số liên tục trên \mathbb R
Với x > 0 thì f\left( x \right) = \left| x \right|\left( {x + 2} \right) = x\left( {x + 2} \right) = {x^2} + 2x
\Rightarrow f'\left( x \right) = 2x + 2 > 0 với mọi x > 0.
Với x < 0 thì f\left( x \right) = \left| x \right|\left( {x + 2} \right) = - x\left( {x + 2} \right) = - {x^2} - 2x
\Rightarrow f'\left( x \right) = - 2x - 2
f'\left( x \right) = 0 \Leftrightarrow x = - 1 và f\left( { - 1} \right) = 1
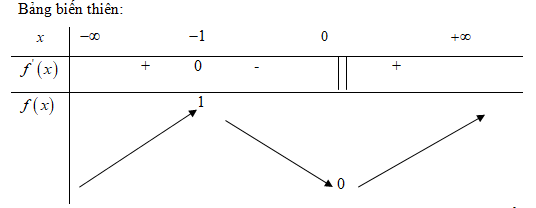
Hàm số đạt cực đại tại x=-1, giá trị cực đại f\left( { - 1} \right) = 1. Hàm số đạt cực tiểu tại điểm x=0, giá trị cực tiểu f\left( 0 \right) = 0
LG e
f\left( x \right) = {{{x^5}} \over 5} - {{{x^3}} \over 3} + 2;
Lời giải chi tiết:
TXĐ: D=\mathbb R
f'\left( x \right) = {x^4} - {x^2} = {x^2}\left( {{x^2} - 1} \right)
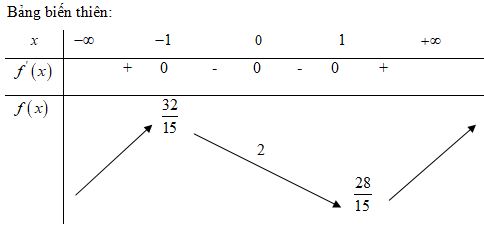
f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = 0;f\left( 0 \right) = 2 \hfill \cr x = - 1;f\left( { - 1} \right) = {{32} \over {15}} \hfill \cr x = 1;f\left( 1 \right) = {{28} \over {15}} \hfill \cr} \right.
Hàm số đạt cực đại tại điểm x=-1, giá trị cực đại f\left( { - 1} \right) = {{32} \over {15}}
Hàm số đạt cực tiểu tại x=1, giá trị cực tiểu f\left( 1 \right) = {{28} \over {15}}
LG f
f\left( x \right) = {{{x^2} - 3x + 3} \over {x - 1}}
Lời giải chi tiết:
TXĐ: D = {\bf{R}}\backslash \left\{ 1 \right\}
y'\left( x \right) = {{\left( {2x - 3} \right)\left( {x - 1} \right) - \left( {{x^2} - 3x + 3} \right)} \over {{{\left( {x - 1} \right)}^2}}} = {{{x^2} - 2x} \over {{{\left( {x - 1} \right)}^2}}}
f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = 0;f\left( 0 \right) = - 3 \hfill \cr x = 2;f\left( 2 \right) = 1 \hfill \cr} \right.
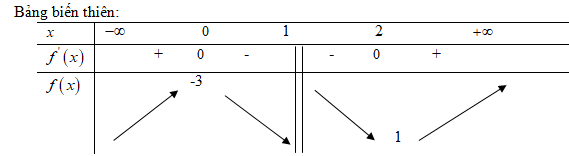
Hàm số đạt cực đại tại điểm x=0, giá trị cực đại f\left( 0 \right) = - 3
Hàm số đạt cực tiểu tại điểm x=2, giá trị cực tiểu f\left( 2 \right) = 1