Đề bài
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. Từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. Biết rằng B đuổi kịp A sau 8 giây (kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
Lời giải chi tiết
Từ công thức v1=v0+at ta có:
Gia tốc trong 8 giây đầu của chất điểm A là:
\(a = \dfrac{{{v_1} - {v_0}}}{t}\) \( = \dfrac{{6 - 0}}{8} = \dfrac{3}{4}\left( {m/{s^2}} \right)\)
⇒ Phương trình vận tốc của chuyển động có dạng:
\(V\left( t \right) = \int {\dfrac{3}{4}dt} = \dfrac{3}{4}t + C\left( {m/{s^2}} \right)\)
Tại t = 0 thì v(0)= 0 nên C= 0.
Do đó,phương trình chuyển động của vật là: \(v\left( t \right) = \dfrac{3}{4}t\)
Trong 8 giây đầu này, chất điểm A chuyển động nhanh dần với vận tốc \(v\left( t \right) = \dfrac{3}{4}t\).
Vậy nó đi được quãng đường là \(\int\limits_0^8 {\dfrac{3}{4}tdt} = \left. {\dfrac{3}{4}.\dfrac{{{t^2}}}{2}} \right|_0^8 = 24\)
Sau 12 giây tiếp theo (khi mà bị B đuổi kịp A), A đi được thêm 6.12 = 72 mét.
Như vậy, khi bị B đuổi kịp, A và B đi được quãng đường là 24 + 72 = 96 mét
Từ công thức \(S = {S_0} + \dfrac{1}{2}a{t^2}\)
Suy ra gia tốc của chất điểm B là: \(a = \dfrac{{2\left( {S - {S_0}} \right)}}{{{t^2}}}\) \( = \dfrac{{2\left( {96 - 0} \right)}}{{{8^2}}} = 3\)
Vậy khi đuổi kịp A, vận tốc của B là:
v1=v0+at=0+3.8=24 (m/s)
Cách khác:
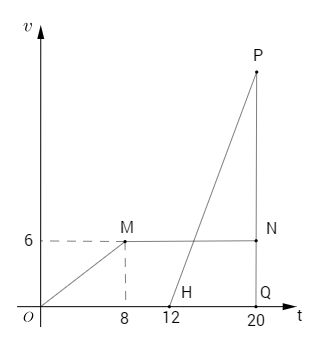
Thời điểm A và B gặp nhau là 20 giây kể từ lúc A xuất phát.
Đồ thị của vận tốc của A là đường gấp khúc OMN.
Quãng đường mà A đi được (s = vt ) là diện tích hình thang OMNQ.
\({S_{OMNQ}} = {1 \over 2}\left( {20 + 12} \right).6 = 96\)
Vậy lúc gặp B, A đi được \(96 m\).
Đồ thị vận tốc của B là đường thẳng HP.
Vì B xuất phát cùng vị trí với A nên B cũng đi được \(96 m\) . Quãng đường B đi được bằng diện tích tam giác \(HPQ\).
Ta có \({S_{HPQ}} = {1 \over 2}.PQ.HQ \) \(\Rightarrow 96 = {1 \over 2}.PQ.8 \Rightarrow PQ = 24.\)
Vậy vận tốc của B tại thời điểm gặp A là \(24\, m/s\).

