Đề bài
Cho khối lăng trụ đểu \(ABC.A'B'C’\) và \(M\) là trung điểm của cạnh \(AB\). Mặt phẳng \((B'C'M)\) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích hai phần đó.
Lời giải chi tiết
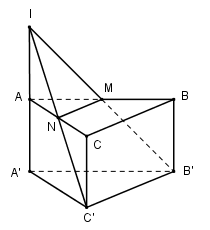
Gọi \(I\) là giao điểm của đường thẳng \(B’M\) với \(AA’\); \(N\) là giao điểm của \(IC’\) với \(AC\). Khi đó \(A\) là trung điểm của \(A’I\) và \(N\) là trung điểm của \(AC\).
Đặt \({S_{ABC}} = S\) và \(AA' = h\)
Thiết diện của mp \((B’C’M)\) với khối lăng trụ \(ABC.A’B’C’\) là hình thang cân \(MNC’B’\). Mp \((B’C’M)\) chia khối lăng trụ thành hai phần, phần chứa cạnh \(AA’\) có thể tích là \({V_1}\), phần còn lại có thể tích là \({V_2}\). Khi đó ta có:
\(\eqalign{
& {V_1} = {V_{AMN.A'B'C'}} \cr &= {V_{I.A'B'C'}} - {V_{I.AMN}} \cr & = \frac{1}{3}{S_{A'B'C'}}.A'I - \frac{1}{3}{S_{AMN}}.AI\cr &= {1 \over 3}S.2h - {1 \over 3}.{S \over 4}h \cr
& = {2 \over 3}Sh - {1 \over {12}}Sh = {7 \over {12}}Sh \cr &= {7 \over {12}}\left( {{V_1} + {V_2}} \right) \cr
& \Rightarrow 12{V_1} = 7{V_1} + 7{V_2}\Leftrightarrow 5{V_1} = 7{V_2}\cr & \Rightarrow {{{V_1}} \over {{V_2}}} = {7 \over 5} \cr} \)
Cách trình bày khác:
Ta có: \(\frac{{IA}}{{IA'}} = \frac{{IM}}{{IB}} = \frac{{IN}}{{IC'}} = \frac{{AM}}{{A'B'}} = \frac{1}{2}\)
\({V_1} = {V_{AMN.A'B'C'}}\) \( = {V_{I.A'B'C'}} - {V_{I.AMN}}\)
\({V_{I.A'B'C'}} = \frac{1}{3}{S_{A'B'C'}}.A'I\) \( = \frac{1}{3}S.2h = \frac{2}{3}Sh = \frac{2}{3}V\)
\(\frac{{{V_{I.AMN}}}}{{{V_{I.A'B'C'}}}} = \frac{{IA}}{{IA'}}.\frac{{IM}}{{IB'}}.\frac{{IN}}{{IC'}}\) \( = \frac{1}{2}.\frac{1}{2}.\frac{1}{2} = \frac{1}{8}\)
\( \Rightarrow {V_{I.AMN}} = \frac{1}{8}{V_{I.A'B'C'}}\) \( = \frac{1}{8}.\frac{2}{3}V = \frac{1}{{12}}V\)
\( \Rightarrow {V_1} = \frac{2}{3}V - \frac{1}{{12}}V = \frac{7}{{12}}V\)
\( \Rightarrow {V_2} = V - {V_1}\) \( = V - \frac{7}{{12}}V = \frac{5}{{12}}V\)
\( \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{7}{{12}}V:\frac{5}{{12}}V = \frac{7}{5}\)
