Đề bài
Chứng minh rằng nếu có phép vị tự tỉ số k biến tứ diện ABCD thành tứ diện A′B′C′D′a thì VA′B′C′D′VABCD=|k|3
Lời giải chi tiết
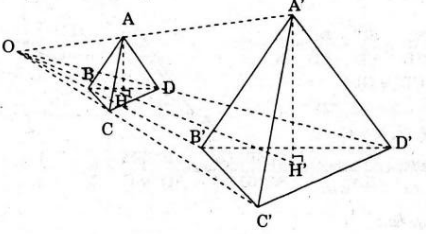
Gọi H là hình chiếu của A trên (BCD).
Giả sử phép vị tự tỉ số k biến A, B, C, D, H lần lượt thành A’, B’, C’, D’, H’.
Hơn nữa, theo tính chất của phép vị tự thì:
A’H’ song song hoặc trùng với AH;
Và (B’C’D’) song song hoặc trùng với (BCD)
Mà AH ⊥ (BCD) nên A'H'⊥(B'C'D').
Vậy A’H’ là đường cao của tứ diện (A’B’C’D’) (1)
Mặt khác, dễ thấy: ^CBD=^C′B′D′=φ (2)
Hơn nữa, cũng từ tính chất của phép vị tự ta có:
A′H′AH=B′C′BC=B′D′BD=|k| (3)
Từ (1), (2), (3) ta có:
VA′B′C′D′VABCD=13SB′C′D′.A′H′13SBCD.AH=SB′C′D′.A′H′SBCD.AH=12B′C′.B′D′sinφ12BC.BDsinφ.A′H′AH=B′C′BC.B′D′BD.A′H′AH=|k|3

