LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số: y=−x3+3x2−1.
Lời giải chi tiết:
TXĐ: D=R
lim
Bảng biến thiên:
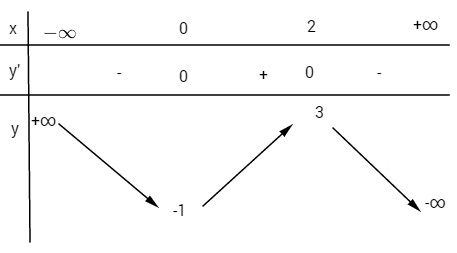
Hàm đồng biến trên khoảng (0;2), nghịch biến trên mỗi khoảng \left( { - \infty ;0} \right) và \left( {2; + \infty } \right).
Hàm số đạt cực tiểu tại điểm x = 0, giá trị cực tiểu y(0) = -1. Hàm số đạt cực đại tại điểm x = 2, giá trị cực đại y(2) = 3.
Đồ thị: y'' = - 6x + 6
y'' = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = 1
Xét dấu y”:
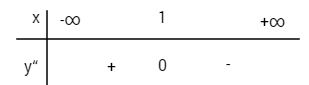
I(1;1) là điểm uốn của đồ thị
Điểm đặc biệt:
x = 0 \Rightarrow y = - 1
x = - 1 \Rightarrow y = 3
LG b
Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình: - {x^3} + 3{x^2} - 1 = m
Lời giải chi tiết:
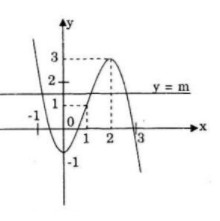
Số nghiệm của phương trình chính là số giao điểm của đồ thị (C) hàm số y = - {x^3} + 3{x^2} - 1 với đường thẳng y = m cùng phương với trục Ox.
Dựa vào đồ thị ở câu a) ta có:
- Nếu m > 3: Phương trình (*) có 1 nghiệm
- Nếu m = 3: Phương trình (*) có 2 nghiệm.
- Nếu -1 < m < 3 : Phương trình (*) có 3 nghiệm
- Nếu m = -1: Phương trình (*) có 2 nghiệm.
- Nếu m < -1 phương trình (*) có 1 nghiệm.
Vậy,
- Nếu m < -1 hoặc m > 3 thì phương trình có 1 nghiệm;
- Nếu m = -1 hoặc m = 3 thì phương trình có 2 nghiệm;
- Nếu -1 < m < 3 thì phương trình có 3 nghiệm.

