Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
LG a
f(x)=x2+2x−5 trên đoạn [−2;3];
Lời giải chi tiết:
D=[−2;3]
f′(x)=2x+2
f′(x)=0⇔x=−1∈[−2;3]
Ta có: f(−2)=−5;f(−1)=−6; f(3)=10.
Vậy: min.
Cách khác:
Hàm số f(x)= x2 + 2x – 5
Tập xác định D = R.
Đạo hàm y’= 2x +2 = 0 ⇔ x = - 1
Bảng biến thiên:
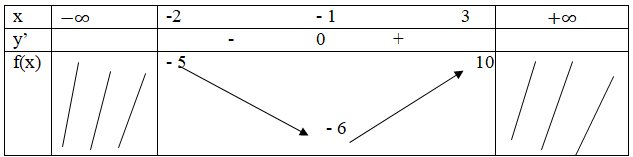
Vậy: \mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 2;3} \right]} = - 6;\mathop {\max \,f\left( x \right) = 10}\limits_{x \in \left[ { - 2;3} \right]} .
LG b
f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x - 4 trên đoạn \left[ { - 4;0} \right];
Lời giải chi tiết:
D = \left[ { - 4;0} \right]
f'\left( x \right) = {x^2} + 4x + 3
f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \in \left[ { - 4;0} \right] \hfill \cr x = - 3 \in \left[ { - 4;0} \right] \hfill \cr} \right.
Ta có: f\left( { - 4} \right) = - {{16} \over 3};f\left( { - 1} \right) = - {{16} \over 3}; f\left( { - 3} \right) = - 4;f\left( 0 \right) = - 4
Vậy \mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]} = - {{16} \over 3}; \mathop {\max \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]} = - 4.
LG c
f\left( x \right) = x + {1 \over x} trên đoạn \left( {0; + \infty } \right);
Lời giải chi tiết:
D = \left( {0; + \infty } \right)
f'\left( x \right) = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}} với mọi x \ne 0
f'\left( x \right) = 0 \Leftrightarrow x = \pm 1
x=1\in \left( {0; + \infty } \right.)
x=-1\not\in \left( {0; + \infty } \right.)
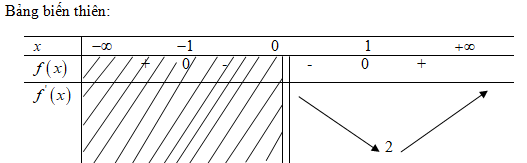
Vậy \mathop {\min \,\,f\left( x \right) = f\left( 1 \right)}\limits_{x \in \left( {0; + \infty } \right)} = 2.
Hàm số không đạt giá trị lớn nhất trên khoảng \left( {0; + \infty } \right).
LG d
f\left( x \right) = - {x^2} + 2x + 4 trên đoạn \left[ {2;4} \right];
Lời giải chi tiết:
D = \left[ {2;4} \right]
f'\left( x \right) = - 2x + 2
f'\left( x \right) = 0 \Leftrightarrow x = 1 \notin \left[ {2;4} \right]
Ta có: f\left( 2 \right) = 4;f\left( 4 \right) = - 4
Vậy \mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = - 4; \mathop {\max f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = 4.
LG e
f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}} trên đoạn \left[ {0;1} \right];
Lời giải chi tiết:
D = \left[ {0;1} \right]
f'\left( x \right) = {{2{x^2} + 8x + 6} \over {{{\left( {x + 2} \right)}^2}}}
f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \notin \left[ {0;1} \right] \hfill \cr x = - 3 \notin \left[ {0;1} \right] \hfill \cr} \right.
Ta có: f\left( 0 \right) = 2;f\left( 1 \right) = {{11} \over 3}
Vậy \mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = 2; \mathop {\max f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = {{11} \over 3}
Cách khác:
Bảng biến thiên:
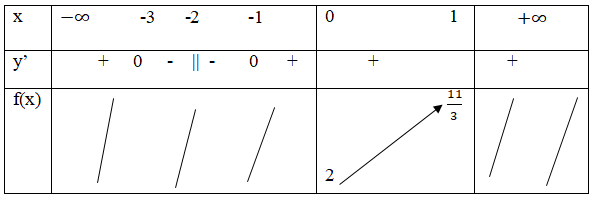
Vậy \mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = 2; \mathop {\max f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = {{11} \over 3}
LG f
f\left( x \right) = x - {1 \over x} trên đoạn \left( {0;2} \right];
Lời giải chi tiết:
D = \left( {0;2} \right]
f'\left( x \right) = 1 + {1 \over {{x^2}}} > 0 với mọi x \in \left( {0;2} \right]
f\left( 2 \right) = {3 \over 2}
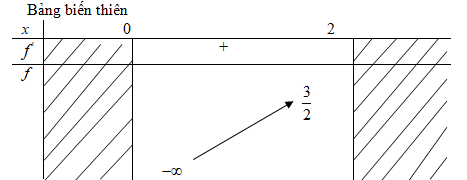
Vậy \mathop {\,\max f\left( x \right)}\limits_{x \in \left[ {0;2} \right]} = {3 \over 2} .
Hàm số không đạt giá trị nhỏ nhất trên \left( {0;2} \right].

