Đề bài
Tính thể tích của khối lăng trụ \(n\)-giác đều có tất cả các cạnh đều bằng \(a\).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích lăng trụ V=Bh.
Lời giải chi tiết
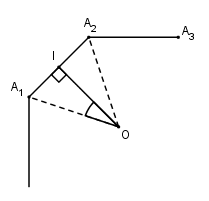
Gọi \({A_1}{A_2}...{A_n}\) là đáy của khối lăng trụ \(n\)-giác đều và \(O\) là tâm của đáy.
Gọi \(I\) là trung điểm của \({A_1}{A_2}\) ta có \(OI \bot {A_1}{A_2}\).
Trong \(\Delta {A_1}IO\): \(\cot \widehat {{A_1}OI} = {{OI} \over {{A_1}I}} \)
\( \Rightarrow OI = {A_1}I\cot \widehat {{A_1}OI}\)
Mà \({A_1}I = \frac{1}{2}{A_1}{A_2} = \frac{a}{2}\) và \(\widehat {{A_1}OI} = \frac{1}{2}\widehat {{A_1}O{A_2}} = \frac{1}{2}.\frac{{2\pi }}{n} = \frac{\pi }{n}\) nên \(OI = \frac{a}{2}.\cot \frac{\pi }{n}\)
\( \Rightarrow {S_{{A_1}O{A_2}}} = \frac{1}{2}OI.{A_1}{A_2}\) \( = \frac{1}{2}.\frac{a}{2}\cot \frac{\pi }{n}.a = \frac{{{a^2}}}{4}\cot \frac{\pi }{n}\)
Diện tích đáy của khối lăng trụ đều là \( {S} = n.{S_{{A_1}O{A_2}}} = \frac{{n{a^2}}}{4}\cot \frac{\pi }{n}\)
Chiều cao của khối lăng trụ đều là \(a\) nên thể tích của nó là:
\( V = Bh = \frac{{n{a^2}}}{4}\cot \frac{\pi }{n}.a = \frac{{n{a^3}}}{4}\cot \frac{\pi }{n}\)

