Chọn đáp án đúng:
5.124
Đạo hàm của hàm số y = x3 - 2x2 + x + 1 tại x = 0 bằng
A. 1 B. 0 C. 2 D. -2
Lời giải chi tiết:
\(\begin{array}{l}y' = 3{x^2} - 4x + 1\\y'\left( 0 \right) = 3.0 - 4.0 + 1 = 1\end{array}\)
Chọn đáp án: A
5.125
Hàm số \(y = \left\{ \begin{array}{l}2x\,voi\,x \ge 0\\ - 3x\,voi\,x < 0\end{array} \right.\) không có đạo hàm tại
A. x = 2 B. x = 1
C. x = 0 D. x = -1
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{y\left( x \right) - y\left( 0 \right)}}{{x - 0}}= \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{2x - 0}}{{x - 0}} = 2\\\mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{y\left( x \right) - y\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{ - 3x - 0}}{{x - 0}} = - 3\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{y\left( x \right) - y\left( 0 \right)}}{{x - 0}}\) \( \ne \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{y\left( x \right) - y\left( 0 \right)}}{{x - 0}}\)
\( \Rightarrow \) Hàm số không có đạo hàm tại \(x = 0\).
Chọn đáp án: C
5.126
Phương trình tiếp tuyến với đồ thị của hàm số y = x3 + 1 tại x = -1 là
A. y = 3x + 2 B. y = 3x - 2
C. y = 3x + 4 D. y = 3x + 3
Lời giải chi tiết:
Ta có: \(y' = 3{x^2}\) \( \Rightarrow y'\left( { - 1} \right) = 3\)
\({x_0} = - 1 \Rightarrow y\left( { - 1} \right) = 0\)
Phương trình tiếp tuyến \(y = 3\left( {x + 1} \right) + 0\) hay \(y = 3x + 3\).
Chọn đáp án: D
5.127
Đạo hàm của hàm số \(y = \dfrac{{2x}}{{\sin x}}\) là
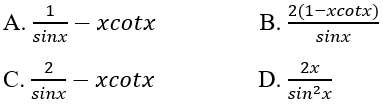
Lời giải chi tiết:
\(\begin{array}{l}y' = \dfrac{{\left( {2x} \right)'\sin x - 2x\left( {\sin x} \right)'}}{{{{\sin }^2}x}}\\ = \dfrac{{2\sin x - 2x\cos x}}{{{{\sin }^2}x}}\\ = \dfrac{{2\sin x}}{{{{\sin }^2}x}} - \dfrac{{2x\cos x}}{{{{\sin }^2}x}}\\ = \dfrac{2}{{\sin x}} - \dfrac{{2x\cot x}}{{\sin x}}\\ = \dfrac{{2 - 2x\cot x}}{{\sin x}}\\ = \dfrac{{2\left( {1 - x\cot x} \right)}}{{\sin x}}\end{array}\)
Chọn đáp án: B
5.128
Cho f(x) = x3/3 - 2x2 + m2x - 5. Tìm tham số m để f'(x) > 0 với mọi x ∈ R
A. m > 2 B. m > 2 hoặc m < -2
C. m < -2 D. m ∈ R
Lời giải chi tiết:
\(f'\left( x \right) = {x^2} - 4x + {m^2}\) có \(\Delta ' = 4 - {m^2}\)
Để \(f'\left( x \right) > 0,\forall x \in \mathbb{R}\) thì \(\left\{ \begin{array}{l}a = 1 > 0\\\Delta ' = 4 - {m^2} < 0\end{array} \right.\) \( \Leftrightarrow 4 - {m^2} < 0\) \( \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < - 2\end{array} \right.\)
Chọn đáp án: B
5.129
Cho f(x) = tan(2x3 - 5). Tìm f'(x)
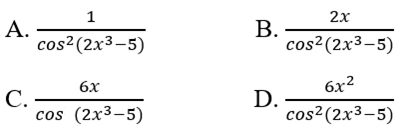
Lời giải chi tiết:
\(\begin{array}{l}f'\left( x \right)\\ = \left( {2{x^3} - 5} \right)'.\dfrac{1}{{{{\cos }^2}\left( {2{x^3} - 5} \right)}}\\ = 2.3{x^2}.\dfrac{1}{{{{\cos }^2}\left( {2{x^3} - 5} \right)}}\\ = \dfrac{{6{x^2}}}{{{{\cos }^2}\left( {2{x^3} - 5} \right)}}\end{array}\)
Chọn đáp án: D
5.130
Tìm nghiệm của phương trình f''(x) = 0 biết f(x) = 3cosx - √3sinx
A. x = π/6 + kπ B. x = π/4 + kπ
C. x = π/3 + kπ D. x = kπ
Phương pháp giải:
HD: Tính f’’(x) rồi giải phương trình tanx = √3.
Lời giải chi tiết:
\(\begin{array}{l}f'\left( x \right) = - 3\sin x - \sqrt 3 \cos x\\f''\left( x \right) = - 3\cos x + \sqrt 3 \sin x\\f''\left( x \right) = 0\\ \Leftrightarrow - 3\cos x + \sqrt 3 \sin x = 0\\ \Leftrightarrow \sqrt 3 \sin x = 3\cos x\\ \Leftrightarrow \sin x = \sqrt 3 \cos x\\ \Leftrightarrow \dfrac{{\sin x}}{{\cos x}} = \sqrt 3 \\ \Leftrightarrow \tan x = \sqrt 3 = \tan \dfrac{\pi }{3}\\ \Leftrightarrow x = \dfrac{\pi }{3} + k\pi ,k \in \mathbb{Z}\end{array}\)
Chọn đáp án: C
5.131
Cho y = tan3x. Tìm dy
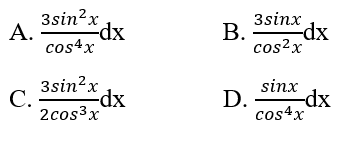
Lời giải chi tiết:
\(\begin{array}{l}y' = 3{\tan ^2}x\left( {\tan x} \right)'\\ = 3{\tan ^2}x.\dfrac{1}{{{{\cos }^2}x}}\\ = 3.\dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}}.\dfrac{1}{{{{\cos }^2}x}}\\ = \dfrac{{3{{\sin }^2}x}}{{{{\cos }^4}x}}\\ \Rightarrow dy = y'dx = \dfrac{{3{{\sin }^2}x}}{{{{\cos }^4}x}}dx\end{array}\)
Chọn đáp án: A

