Đề bài
Chứng minh rằng mỗi phép quay đều có thể xem là kết quả của việc thực hiện liên tiếp hai phép đối xứng trục.
Phương pháp giải - Xem chi tiết
- Cho \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M’\) sao cho \(OM’=OM\) và góc lượng giác \((OM;OM’)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).
Lời giải chi tiết
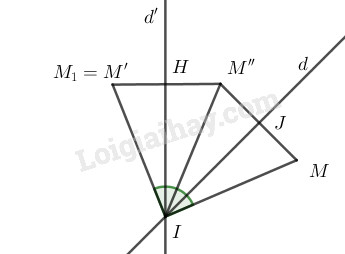
Gọi \(Q_{(I,\alpha)}\) là phép quay tâm \(I\) góc \(\alpha\). Lấy đường thẳng \(d\) bất kì qua \(I\). Gọi \(d’\) là ảnh của \(d\) qua phép quay tâm \(I\) góc \(\dfrac{\alpha}{2}\). Lấy điểm \(M\) bất kì và gọi \(M’=Q_{(I,\alpha)}(M)\). Gọi \(M’’\) là ảnh của \(M\) qua phép đối xứng qua trục \(d\). \(M_1\) là ảnh của \(M’’\) qua phép đối xứng qua trục \(d’\). Gọi \(J\) là giao của \(MM’\) với \(d\), \(H\) là giao của \(M’’M_1\) với \(d’\).
Khi đó ta có đẳng thức giữa các góc lượng giác sau:
\((IM,IM_1)\)
\(=(IM,IM’’)+(IM’’,IM_1)\)
\(=2(IJ,IM’’)+2(IM’’,IH)\)
\(=2(IJ,IH)=2\dfrac{\alpha}{2}=\alpha=(IM,IM’)\)
Từ đó suy ra \(M’\equiv M_1\). Như vậy \(M’\) có thể xem là ảnh của \(M\) sau khi thực hiện liên tiếp hai phép đối xứng qua hai trục \(d\) và \(d’\).