Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}\,neu\,x \ge 0\\{x^2} - 1\,neu\,x < 0\end{array} \right.\)
LG a
a) Vẽ đồ thị của hàm số f(x). Từ đó dự đoán về giới hạn của f(x) khi x → 0
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = {x^2}\) và \(y = {x^2} - 1\) trên cùng một hệ trục tọa độ.
Khi \(x \ge 0\) thì \(f\left( x \right) = {x^2}\) nên xóa nhánh đồ thị \(y = {x^2}\) bên trái trục tung đi.
Khi \(x < 0\) thì \(f\left( x \right) = {x^2} - 1\) nên xóa nhánh đồ thị \(y = {x^2} - 1\) bên phải trục tung đi.
Ta được đồ thị hàm số \(y = f\left( x \right)\).
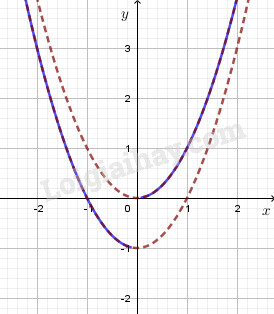
Từ đồ thị ta thấy hàm số không có giới hạn khi \(x \to 0\).
LG b
b) Dùng định nghĩa chứng minh dự đoán trên.
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\)
Lấy dãy \(\left\{ {{x_n}} \right\}\) và \(\left\{ {{y_n}} \right\}\) thỏa mãn \({x_n} = \dfrac{1}{n}\) và \({y_n} = - \dfrac{1}{n}\)
Dễ thấy \(\lim {x_n} = 0,\lim {y_n} = 0\).
Ta có:
Vì \({x_n} = \dfrac{1}{n} > 0\) nên \(\lim f\left( {{x_n}} \right) = \lim x_n^2 = \lim \dfrac{1}{{{n^2}}} = 0\)
Vì \({y_n} = - \dfrac{1}{n} < 0\) nên \(\lim f\left( {{y_n}} \right) = \lim \left( {y_n^2 - 1} \right)\)\( = \lim \left[ {{{\left( { - \dfrac{1}{n}} \right)}^2} - 1} \right]\) \( = \lim \left[ {\dfrac{1}{{{n^2}}} - 1} \right] = 0 - 1 = - 1\)
Do \(\lim f\left( {{x_n}} \right) \ne \lim f\left( {{y_n}} \right)\) nên không tồn tại giới hạn hàm số khi \(x \to 0\).

