Đề bài
Trong không gian cho điểm O và bốn điểm A,B,C,D phân biệt và không thẳng hàng. Chứng minh rằng điều kiện cần và đủ để bốn điểm A,B,C,D tạo thành một hình bình hành là:
→OA+→OC=→OB+→OD
Phương pháp giải - Xem chi tiết
ABCD là hình bình hành nếu và chỉ nếu →BC=→AD
Lời giải chi tiết
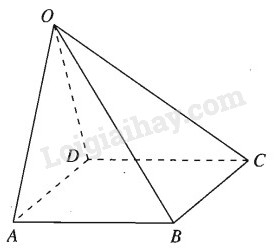
Giả sử bốn điểm A,B,C,D tạo thành một hình bình hành ta có:
→BC=→AD ⇔→OC−→OB=→OD−→OA (với điểm O bất kì )
⇔→OC+→OA=→OD+→OB
Ngược lại, giả sử ta có hệ thức:
→OC+→OA=→OD+→OB
⇔→OC−→OB=→OD−→OA
⇔→BC=→AD
Vì A,B,C,D không thẳng hàng nên tứ giác ABCD là hình bình hành.

