Đề bài
Cho hình chóp tứ giác đều S.ABCD. Gọi M, N lần lượt là trung điểm của SA và SC.
a) Chứng minh AC ⊥ SD
b) Chứng minh MN ⊥ (SBD)
c) Cho AB = SA = a. Tính cosin của góc giữa (SBC) và (ABCD)
Lời giải chi tiết
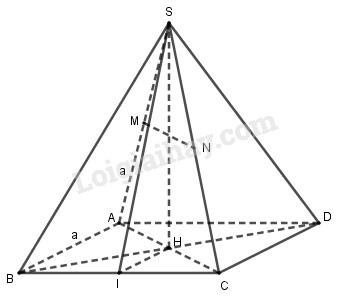
a) Gọi H là tâm hình vuông ABCD \( \Rightarrow SH \bot \left( {ABCD} \right)\).
Ta có: AC ⊥ SH & AC ⊥ BD
⇒ AC ⊥ (SBD) ⇒ AC ⊥ SD.
b) MN là đường trung bình của tam giác SAC nên MN//AC.
Mà AC ⊥ (SBD) ⇒ MN ⊥ (SBD).
c) + Xác định góc α giữa (SBC) và (ABCD)
Gọi I là trung điểm của BC, ta có:
BC ⊥ IH & BC ⊥ SH ⇒ BC ⊥ (SIH)
⇒ BC ⊥ SI.
Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\SI \bot BC\\HI \bot BC\end{array} \right.\) nên góc giữa (SBC) và (ABCD) là góc giữa SI và HI hay \(\widehat {SIH} = \alpha \).
+ Tính α:
Ta có: \(IH = \dfrac{1}{2}AB = \dfrac{a}{2}\)
\(SI = \sqrt {S{C^2} - I{C^2}} \) \( = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\)
\( \Rightarrow \cos \alpha = \dfrac{{IH}}{{SI}} = \dfrac{a}{2}:\dfrac{{a\sqrt 3 }}{2} = \dfrac{1}{{\sqrt 3 }}\)

