Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−2y−6=0
LG câu a
Viết phương trình của đường thẳng d1 là ảnh của d qua phép đối xứng qua trục Oy
Phương pháp giải:
Sử dụng biểu thức tọa độ của phép đối xứng trục Oy: {x′=−xy′=y.
Lời giải chi tiết:
Với mỗi điểm M(x;y) bất kì thuộc d, gọi M′(x′;y′)=DOy(M)
Khi đó {x′=−xy′=y⇔{x=−x′y=y′.
Mà M(x;y)∈d:3x−2y−6=0 nên 3.(−x′)−2.y′−6=0 hay 3x′+2y′+6=0.
Vậy d1:3x+2y+6=0.
LG câu b
Viết phương trình của đường thẳng d2 là ảnh của d qua phép đối xứng qua đường thẳng Δ có phương trình x+y−2=0.
Phương pháp giải:
– Tìm giao điểm A của d và Δ.
- Lấy một điểm B∈d, tìm ảnh B′ của B qua DΔ.
- Viết phương trình AB′ và kết luận.
Lời giải chi tiết:
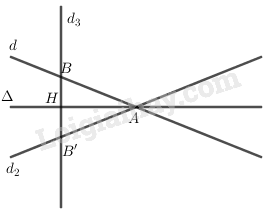
Dễ thấy Δ và d cắt nhau do 31≠−21 nên gọi A(x;y)=d∩Δ.
Tọa độ của A thỏa mãn hệ phương trình {3x−2y−6=0x+y−2=0 ⇔{3x−2y=6x+y=2⇔{x=2y=0
⇒A(2;0).
Lấy B(0;−3)∈d, gọi B′(x;y)=DΔ(B), ta tìm tọa độ B′.
Gọi d3 là đường thẳng qua B(0;−3) và vuông góc Δ. Khi đó →nd3⊥→nd⇒→nd3=(1;−1).
Phương trình d3:1(x−0)−1(y+3)=0 hay x−y−3=0.
Gọi H=Δ∩d3 thì tọa độ của H thỏa mãn hệ phương trình {x+y−2=0x−y−3=0⇔{x=52y=−12
⇒H(52;−12).
Mà B′=DΔ(B) nên H là trung điểm của BB′
⇒{xB′=2xH−xByB′=2yH−yB
hay
{xB′=2.52−0=5yB′=2.(−12)−(−3)=2
⇒B′(5;2).
Đường thẳng d2 đi qua hai điểm A(2;0) và B′(5;2) nên có phương trình x−25−2=y−02−0 hay 2x−3y−4=0.
Vậy d2:2x−3y−4=0.

