Đề bài
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy.
a) Chứng minh tam giác SBC vuông
b) Gọi H là chân đường cao vẽ từ B của tam giác ABC.
Chứng minh (SAC) ⊥ (SBH)
c) Cho AB = a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)
Lời giải chi tiết
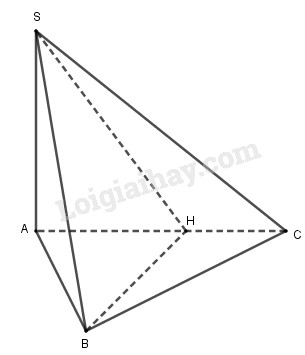
a) Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)
Mà \(BC \bot AB\) nên \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)
\( \Rightarrow \Delta SBC\) vuông tại B.
b) Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BH\)
Mà \(BH \bot AC\) nên \(BH \bot \left( {SAC} \right)\)
Lại có \(\left\{ \begin{array}{l}BH \subset \left( {SBH} \right)\\BH \bot \left( {SAC} \right)\end{array} \right. \Rightarrow \left( {SBH} \right) \bot \left( {SAC} \right)\)
c) Do \(BH \bot \left( {SAC} \right)\) nên \(d\left( {B,\left( {SAC} \right)} \right) = BH\).
Tam giác \(ABC\) vuông tại B đường cao BH nên:
\(\dfrac{1}{{B{H^2}}} = \dfrac{1}{{B{A^2}}} + \dfrac{1}{{B{C^2}}}\) \( = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{5}{{4{a^2}}}\) \( \Rightarrow B{H^2} = \dfrac{{4{a^2}}}{5}\) \( \Rightarrow BH = \dfrac{{2a}}{{\sqrt 5 }} = \dfrac{{2a\sqrt 5 }}{5}\)

