Đề bài
Dựng tam giác BAC vuông cân tại A có C là một điểm cho trước, còn hai đỉnh A,B lần lượt thuộc hai đường thẳng a,b song song với nhau cho trước.
Phương pháp giải - Xem chi tiết
- Giả sử dựng được hình vẽ.
- Sử dụng tính chất hình học đã biết suy ra cách dựng.
Lời giải chi tiết
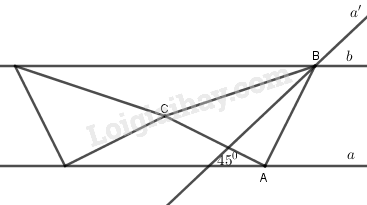
Ta có: ΔBAC vuông cân tại A nên ^ACB=450.
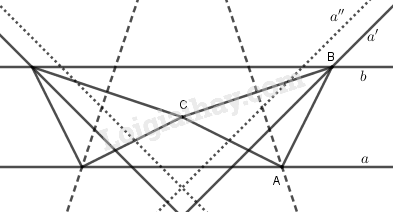
Xem B là ảnh của A qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm C góc ±450 và phép vị tự tâm C tỉ số k=√2.
Vì A thuộc a nên B thuộc đường thẳng a′ là ảnh của a qua phép đồng dạng nói trên. Vậy B là giao của a′ và b.
Từ đó suy ra cách dựng:
- Dựng đường thẳng a″ là ảnh của a qua phép quay tâm C góc quay \pm {45^0}.
- Dựng đường thẳng a' là ảnh của a'' qua phép vị tự tâm C tỉ số \sqrt 2 .
- Lấy B = a' \cap b.
- Dựng đường trung trực của BC, đường này cắt a tại A.
Bài toán có hai nghiệm hình.