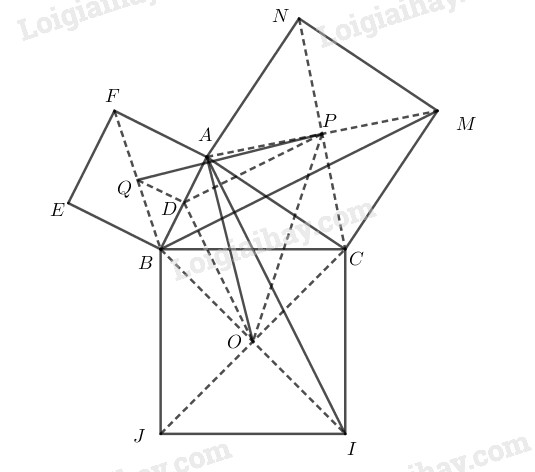
Cho tam giác ABC. Dựng về phía ngoài của tam giác các hình vuông BCIJ, ACMN, ABEFvà gọi O, P, Q lần lượt là tâm đối xứng của chúng
LG a
Gọi D là trung điểm của AB. Chứng minh rằng DOP là tam giác vuông cân đỉnh D
Phương pháp giải:
Sử dụng định nghĩa:
Cho O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M′ sao cho OM′=OM và góc lượng giác (OM;OM′) bằng α được gọi là phép quay tâm O góc α.
Sử dụng tính chất phép quay biến một đoạn thẳng thành đoạn thẳng bằng đoạn thẳng đã cho.
Lời giải chi tiết:
Q(C;900)(M)=AQ(C;900)(B)=I
Do đó phép quay tâm C góc 90o biến MB thành AI.
Nên MB bằng và vuông góc với AI.
Tam giác ABM có DP là đường trung bình nên DP//BM và DP=12BM.
Tam giác ABI có DO là đường trung bình nên DO//AI và DO=12AI
Từ đó suy ra DP⊥DO và DP=DO.
Vậy tam giác DPO vuông tại D.
LG b
Chứng minh AO vuông góc với PQ và AO=PQ
Phương pháp giải:
Sử dụng định nghĩa:
Cho O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M′ sao cho OM′=OM và góc lượng giác (OM;OM′) bằng α được gọi là phép quay tâm O góc α.
Sử dụng tính chất phép quay biến một đoạn thẳng thành đoạn thẳng bằng độ dài đoạn thẳng đã cho.
Lời giải chi tiết:
Ta có:
\Q(D;900)(A)=QQ(D;900)(O)=P
Do đó phép quay tâm D góc quay 900 biến AO thành QP.
Do đó OA bằng và vuông góc với PQ.

