Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Gọi O là giao điểm của AC và BD, O′ là giao điểm của AE và BF.
LG a
Chứng minh rằng OO′ song song với hai mặt phẳng (ADF) và (BCE)
Phương pháp giải:
Sử dụng tính chất hình bình hành có giao điểm của hai đường chéo cắt nhau tại trung điểm mỗi đường.
Sử dụng tính chất đường trung bình của tam giác.
Sử dụng tính chất: Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d′ nằm trong (α) thì d song song (α).
Lời giải chi tiết:
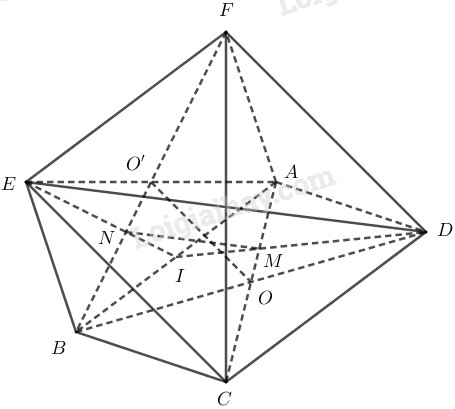
Ta có tứ giác ABCD là hình bình hành, O=AC∩BD nên O là trung điểm của AC,BD.
Tứ giác ABEF là hình bình hành, O′=AE∩BF nên O′ là trung điểm của AE,BF
Xét tam giác BFD có O là trung điểm của BD, O′ là trung điểm của BF
Theo tính chất đường trung bình của tam giác ta có OO′∥DF
Mà DF⊂(ADF)
⇒OO′∥(ADF)
Xét tam giác ACE có O là trung điểm của AC, O′ là trung điểm của AE
Theo tính chất đường trung bình của tam giác ta có OO′∥CE
Mà CE⊂(BCE)
⇒OO′∥(BCE).
LG câu b
Gọi M và N lần lượt là trọng tâm của các tam giác ABD và ABE. Chứng minh rằng MN∥(CEF).
Phương pháp giải:
Sử dụng tính chất trọng tâm của tam giác.
Sử dụng định lý Talet.
Sử dụng tính chất: Nếu hai mặt phẳng lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Lời giải chi tiết:
Gọi I là trung điểm AB.
Trong tam giác ABD có M là trọng tâm nên ta có IMID=13.
Trong tam giác ABE có N là trọng tâm nên ta có INIE=13.
Suy ra IMID=INIE=13.
Theo định lý Talet suy ra MN∥DE(1)
Mà do tứ giác ABCD là hình bình hành nên AB∥=CD
Và tứ giác ABEF là hình bình hành nên AB∥=EF
Suy ra CD∥=EF ⇒CEFD là hình bình hành DE⊂(CEF)(2)
Từ (1) và (2) ⇒MN∥(CEF).

