Đề bài
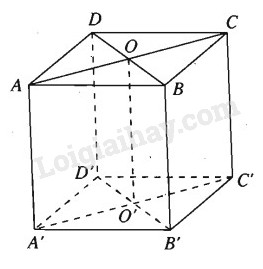
Cho hình lập phương ABCDA’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.
a) Hãy biểu diễn các vectơ \(\overrightarrow {AO} ,\overrightarrow {AO'} \) theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.
b) Chứng minh rằng \(\overrightarrow {A{\rm{D}}} + \overrightarrow {D'C'} + \overrightarrow {D'A'} = \overrightarrow {AB} \).
Phương pháp giải - Xem chi tiết
Xen các điểm thức hợp và sử dụng các tính chất cộng véc tơ, quy tắc trung điểm,... để biểu diễn một véc tơ qua ba véc tơ không đồng phẳng trong không gian.
Lời giải chi tiết
a) *\(\displaystyle \overrightarrow {AO} = {1 \over 2}\overrightarrow {AC} = {1 \over 2}\overrightarrow {A'C'} \) \(\displaystyle = {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {A{\rm{D}}} } \right)\)
\(\displaystyle \overrightarrow {AO} = \overrightarrow {AB} + \overrightarrow {BO} = \overrightarrow {AB} + {1 \over 2}\overrightarrow {B{\rm{D}}} ,....\)
*\(\displaystyle \overrightarrow {AO} = {1 \over 2}\overrightarrow {AC} + \overrightarrow {AA'} \)
\(\displaystyle \eqalign{
& = {1 \over 2}\left( {\overrightarrow {AA'} + \overrightarrow {AC'} } \right) = {1 \over 2}\left( {\overrightarrow {AB'} + \overrightarrow {AD'} } \right) \cr
& = \overrightarrow {AA'} + \overrightarrow {A'B'} + {1 \over 2}\overrightarrow {B'D'} \cr
& = \overrightarrow {AB} + \overrightarrow {BB'} + {1 \over 2}\overrightarrow {B'D'} ,... \cr} \)
b) \(\displaystyle \overrightarrow {AD} + \overrightarrow {D'C'} + \overrightarrow {D'A'}\) \(\displaystyle = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {CB} \)
(vì \(\displaystyle \overrightarrow {D'C'} = \overrightarrow {DC} \) và \(\displaystyle \overrightarrow {D'A'} = \overrightarrow {CB} \)) nên \(\displaystyle \overrightarrow {A{\rm{D}}} + \overrightarrow {D'C'} + \overrightarrow {D'A'} = \overrightarrow {AB} \).
