Đề bài
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến d. Trong (α) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài (α) và (β) sao cho OA và OB lần lượt cắt (β) tại A′ và B′.
a) Chứng minh ba điểm I, A′, B′ thẳng hàng.
b) Trong (α) lấy điểm C sao cho A, B, C không thẳng hàng. Giả sử OC cắt (β) tại C′, BC cắt B′C′ tại J, CA cắt C′A′ tại K. Chứng minh I, J, K thẳng hàng.
Phương pháp giải - Xem chi tiết
Để chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó cùng thuộc hai mặt phẳng phân biệt.
Lời giải chi tiết
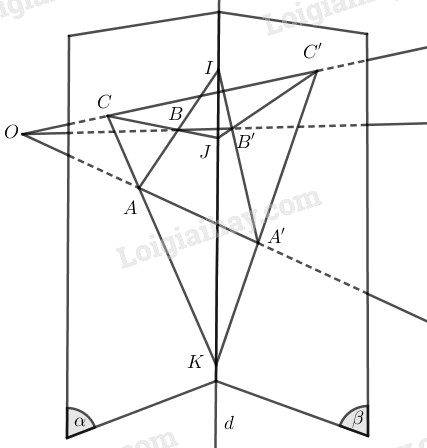
a) Ta có AB∩d=I
Khi đó I∈AB,AB⊂(OAB)⇒I∈(OAB) và I∈d,d⊂(β)⇒I∈(β)
Suy ra I=(OAB)∩(β)
Ta có A′=OA∩(β)
Khi đó A′∈OA,OA⊂(OAB)
⇒A′∈(OAB) và A′∈(β)
Suy ra A′=(OAB)∩(β)
Chứng minh tương tự B′=(OAB)∩(β)
Vậy I, A′, B′ là ba điểm chung của hai mặt phẳng (OAB) và (β) nên chúng thẳng hàng.
b) Ta có I=AB∩d khi đó I∈AB,AB⊂(ABC)⇒I∈(ABC)
Và I∈d,d⊂(β)⇒I∈(β) mà A′,B′,C′∈(β) ⇒(A′B′C′) là (β) nên I∈(A′B′C′)
Suy ra I∈(ABC)∩(A′B′C′)
Ta có BC∩B′C′=J
Khi đó J∈BC,BC⊂(ABC)⇒J∈(ABC) và J∈B′C′,B′C′⊂(A′B′C′)
⇒J∈(A′B′C′)
Suy ra J∈(ABC)∩(A′B′C′)
Tương tự ta có K∈(ABC)∩(A′B′C′)
Vậy I, J, K là ba điểm chung của hai mặt phẳng (ABC) và (A′B′C′) nên chúng thẳng hàng.
