Đề bài
Cho hàm số \(f\left( x \right) = {{\left( {x - 1} \right)\left| x \right|} \over x}\)
Vẽ đồ thị của hàm số này. Từ đồ thị dự đoán các khoảng trên đó hàm số liên tục và chứng minh dự đoán đó.
Phương pháp giải - Xem chi tiết
- Đưa hàm số về dạng khoảng rồi vẽ đồ thị.
- Quan sát đồ thị nhận xét tính liên tục và kết luận.
Lời giải chi tiết
\(f\left( x \right) = {{\left( {x - 1} \right)\left| x \right|} \over x} = \left\{ \matrix{x - 1,\,{\rm{ nếu }}\,\,x > 0 \hfill \cr 1 - x,\,{\rm{ nếu\,\, x < 0}} \hfill \cr} \right.\) Hàm số này có tập xác định là \(R\backslash \left\{ 0 \right\}\)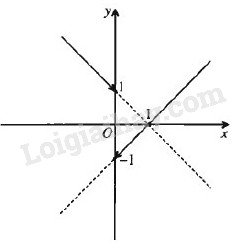
Từ đồ thị dự đoán \(f\left( x \right)\) liên tục trên các khoảng \(\left( { - \infty {\rm{ }};{\rm{ }}0} \right),\;\left( {0{\rm{ }};{\rm{ }} + \infty } \right)\) nhưng không liên tục trên R.
Thật vậy,
- Với \(x > 0,f\left( x \right) = x - 1\) là hàm đa thức nên liên tục trên R do đó liên tục trên \(\left( {0{\rm{ }};{\rm{ }} + \infty } \right)\)
- Với \(x < 0,f\left( x \right) = 1 - x\) cũng làhàmđa thức nên liên tục trên R do đó liên tục trên \(\left( { - \infty {\rm{ }};{\rm{ }}0} \right)\)
Dễ thấy hàm số gián đoạn tại x = 0 vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = - 1,{\rm{ }}\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = 1\)

