Đề bài
Cho hai đường tròn có cùng tâm O, bán kính lần lượt là R và r,(R>r). A là một điểm thuộc đường tròn bán kính r. Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C,D sao cho CD=3AB
Phương pháp giải - Xem chi tiết
- Giả sử dụng được hai điểm C,D thỏa mãn bài toán.
- Sử dụng kiến thức hình học đã biết để suy ra cách dựng.
Lời giải chi tiết
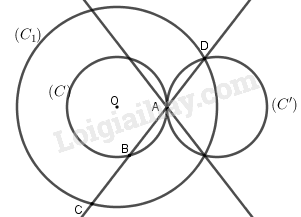
Gọi (C) là đường tròn tâm O bán kính r, (C1) là đường tròn tâm O bán kính R.
Giả sử đường thẳng đã dựng được. Khi đó DA=AB=BC nên D=DA(B).
Mà B∈(C) nên D∈(C′) là ảnh của (C) qua phép đối xứng qua tâm A.
Lại có D∈(C) (giả thiết) nên D=(C′)∩(C1).
Từ đó ta có cách dựng:
+) Dựng ảnh (C′) của (C) qua phép đối xứng tâm A.
+) Nếu (C′) không cắt (C1) thì không có điểm C,D thỏa mãn bài toán.
+) Nếu (C′) tiếp xúc (C1) tại duy nhất một điểm thì có một cặp điểm C,D thỏa mãn bài toán.
+) Nếu (C′) cắt (C1) tại hai điểm phân biệt thì có hai cặp điểm C,D thỏa mãn bài toán.

