Cho hình chóp \(S.ABCD\) có đáy là hình bình hành \(ABCD\), \(O\) là giao điểm hai đường chéo, \(AC = a\), \(BD = b\), tam giác \(SBD\) đều. Gọi \(I\) là điểm di động trên đoạn \(AC\) với \(AI=x\) \((0<x<a)\). Lấy \(\alpha\) là mặt phẳng đi qua \(I\) và song song với mặt phẳng \((SBD)\).
LG a
Xác định thiết diện của mặt phẳng \(\alpha\) với hình chóp \(S.ABCD\)
Phương pháp giải:
Xác định thiết diện của mẳt phẳng \((\alpha)\) với mộ thình chóp khi biết \((\alpha)\) song song với một mặt phẳng nào đó trong hình chóp.
- Sử dụng tính chất khi \((\alpha)\) song song với \((\beta)\) thì \((\alpha)\) sẽ song song với mọi đường thẳng thuộc \((\beta)\).
- Tìm đường thẳng \(d\) nằm trong mặt phẳng \((\beta)\).
- Vì \((\alpha)\parallel d\) nên \((\alpha)\) cắt những mặt phẳng chứa \(d\) theo các giao tuyến song song với \(d\).
Lời giải chi tiết:
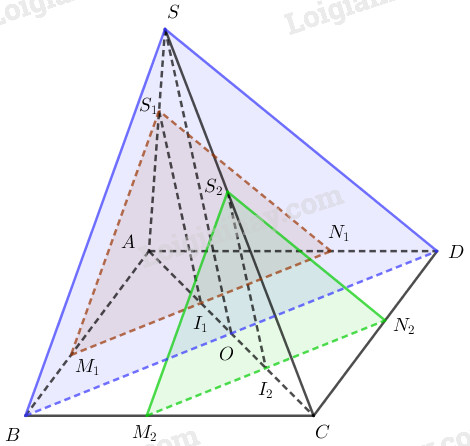
Trường hợp 1: \(I\) thuộc đoạn \(AO\) \((0<x<\dfrac{a}{2})\).
Khi đó \(I\) nằm ở vị trí \(I_1\).
Ta có: \((\alpha)\parallel (SBD)\)
\( \Rightarrow \left\{ \begin{array}{l}(\alpha )\parallel BD\\(\alpha )\parallel SO\end{array} \right.\)
Vì \((\alpha)\parallel BD\) nên \((\alpha)\) cắt \((ABD)\) theo giao tuyến \(M_1N_1\) qua \(I_1\) song song với \(BD\).
Vì \((\alpha)\parallel SO\) nên \((\alpha)\) cắt \((SOA)\) theo giao tuyến \(S_1I_1\) song song với \(SO\).
Nên ta có thiết diện trong trường hợp này là tam giác \(S_1M_1N_1\).
Trường hợp 2: \(I\) thuộc đoạn \(OC\) \((\dfrac{a}{2}<x<a)\).
Khi đó \(I\) nằm ở vị trí \(I_2\).
Tương tự thiết diện trong trường hợp này là tam giác \(S_2M_2N_2\) trong đó \(M_2N_2\parallel BD\), \(S_2M_2\parallel SB\), \(S_2N_2\parallel SD\).
Trường hợp 3: \(I\equiv O\) khi đó thiết diện là tam giác \(SBD\).
LG b
Tìm diện tích \(S\) của thiết diện ở câu a) theo \(a\), \(b\), \(x\). Tìm \(x\) để \(S\) lớn nhất
Phương pháp giải:
Sử dụng công thức tích hai cạnh kề nhân \(sin\) góc xen giữa để tính điên tích tam giác.
Sử dụng giả thiết đề bài cho là \(SBD\) là tam giác đều.
Sử dụng tỉ lệ diện tích để tính.
Vẽ đồ thị hàm số dạng Parabol \(y=x^2\).
Lời giải chi tiết:
Trường hợp 1: \(I\) thuộc đoạn \(OA\) \((0<x<\dfrac{a}{2})\)
Ta có: \(\dfrac{S_{S_1M_1N_1}}{S_{SBD}}={\left({\dfrac{M_1N_2}{BD}}\right)}^2={\left({\dfrac{2x}{a}}\right)}^2\)
\(\Rightarrow S_{S_1M_1N_1}={\left({\dfrac{M_1N_1}{BD}}\right)}^2S_{SBD}\)
\(=\dfrac{4x^2}{a^2}.\dfrac{b^2\sqrt{3}}{4}=\dfrac{b^2x^2\sqrt{3}}{a^2}\).
Trường hợp 2: \(I\) thuộc đoạn \(OA\) \((\dfrac{a}{2}<x<a)\)
Ta có: \(\dfrac{S_{S_1M_1N_1}}{S_{SBD}}={\left({\dfrac{M_1N_2}{BD}}\right)}^2\)
\(={\left[{\dfrac{2(a-x)}{a}}\right]}^2\)
\(\Rightarrow S_{S_2M_2N_2}={\left({\dfrac{M_2N_2}{BD}}\right)}^2S_{SBD}\)
\(=\dfrac{4{(a-x)}^2}{a^2}.\dfrac{b^2\sqrt{3}}{4}=\dfrac{b^2{(a-x)}^2\sqrt{3}}{a^2}\).
Trường hợp 3. \(I\equiv O\) \(S_{SBD}=\dfrac{b^2\sqrt{3}}{4}\).
Vậy \({S_\text{thiết diện}} \)
\(= \left\{ \begin{array}{l}\dfrac{{{b^2}{x^2}\sqrt 3 }}{{{a^2}}}\text{ nếu }0 < x < \dfrac{a}{2}\\\dfrac{{{b^2}\sqrt 3 }}{4}\text{ nếu } x= \dfrac{a}{2}\\\dfrac{{{b^2}{{(a - x)}^2}\sqrt 3 }}{{{a^2}}}\text{ nếu }\dfrac{a}{2} < x < a\end{array} \right.\)
Đồ thị của hàm số \(S\) theo biến \(x\) như sau:
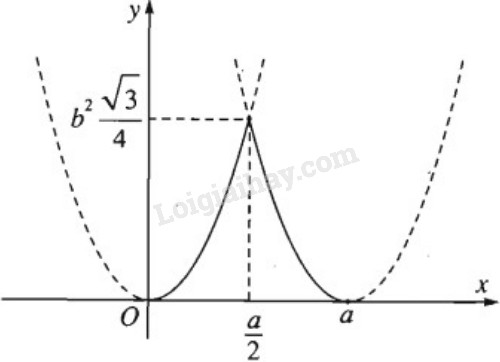
Vậy \({S_\text{thiết diện}} \) lớn nhất là \(b^2\dfrac{\sqrt{3}}{4}\) khi và chỉ khi \(x=\dfrac{a}{2}\).

