Đề bài
Trong mặt phẳng Oxy cho điểm M(1;1). Ảnh của M qua phép quay tâm O, góc quay 450 có tọa độ
A. (−1;1) B. (1;0)
C. (√2;0) D. (0;√2)
Phương pháp giải - Xem chi tiết
Dựng hình và nhận xét.
Lời giải chi tiết
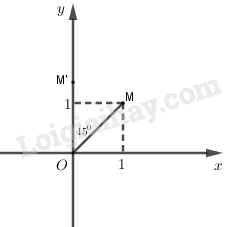
Dễ thấy M(1;1) nằm trên đường phân giác của góc phần tư thứ nhất.
Khi đó M′=Q(O,450)(M) ⇔(OM,OM′)=450 nên M′ nằm trên tia Oy.
Do đó M′(0;m) với m>0.
Lại có OM=OM′ ⇔√2=√0+m2⇔m=√2.
Vậy M′(0;√2).
Chọn D.

