Đề bài
Trong mặt phẳng \(Oxy\) cho đường thẳng \(d\) có phương trình \(x + y - 2 = 0\). Hãy viết phương trình của đường thẳng \(d'\) là ảnh của \(d\) qua phép quay tâm \(O\) góc \(45^\circ \).
Phương pháp giải - Xem chi tiết
- Lấy điểm \(H\left( {1;1} \right)\) thuộc \(d\).
- Tìm ảnh \(H' = {Q_{\left( {O,{{45}^0}} \right)}}\left( H \right)\).
- Viết phương trình đường thẳng đi qua \(H'\) và vuông góc \(OH'\) rồi kết luận.
Lời giải chi tiết
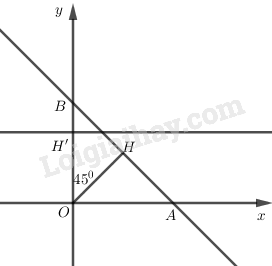
Lấy \(H\left( {1;1} \right) \in d\) và \(OH \bot d\) \( \Rightarrow \) góc giữa \(OH\) và trục \(Oy\) bằng \({45^0}\).
Gọi \(H' = {Q_{\left( {O,{{45}^0}} \right)}}\left( H \right)\) thì \(H' \in Oy\) và \(OH' = OH = \sqrt 2 \) nên \(H' = \left( {0;\sqrt 2 } \right)\).
Từ đó suy ra \(d'\) phải qua \(H'\) và vuông góc với \(OH'\).
Vậy phương trình của \(d'\) là \(y = \sqrt 2 \).

