Giải bài 2.25 trang 77 SBT hình học 11

148 lượt xem

Lựa chọn câu để xem lời giải nhanh hơn

Cho hình lăng trụ tam giác $ABC.A’B’C’$ có các cạnh bên là $AA’$ , $BB’$ , $CC’$ . Gọi $I$ và $I’$ tương ứng là trung điểm của hai cạnh $BC$ và $B’C’$ .

LG a

Chứng minh rằng $AI\parallel A'I'$ .

Phương pháp giải:

Sử dụng tính chất đường trung bình của hình bình hành.

Tính chất hình bình hành.

Lời giải chi tiết:

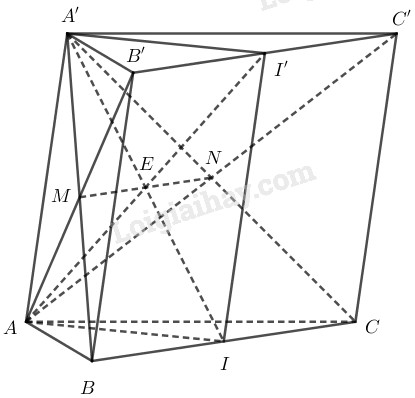
Trong hình bình hành $BB’C’C$ ta có $I, I’$ lần lượt là trung điểm của $BC, B'C'$ nên $II’$ là đường trung bình của hình bình hành $BB’C’C$ .

Suy ra $II’\parallel = BB’$ , mà $AA’\parallel = BB’$ nên $II’\parallel =AA’$ .

Vậy tứ giác $AA’I’I$ là hình bình hành nên $AI\parallel A’I’$ .

LG b

Tìm giao điểm của $IA’$ với mặt phẳng $(AB’C’)$ .

Phương pháp giải:

Muốn tìm giao điểm của đường thẳng $d$ với mặt phẳng $(\alpha)$ ta tìm giao điểm của đường thẳng $d$ với đường thẳng $d’$ , trong đó $d’\subset (\alpha)$ và $d,d’$ cùng thuộc một mặt phẳng.

Lời giải chi tiết:

Ta có: $\left\{ \begin{array}{l}A \in \left( {AB'C'} \right)\\A \in \left( {AA'I'I} \right)\end{array} \right.$ $\Rightarrow A \in \left( {AB'C'} \right) \cap \left( {AA'I'I} \right)$

Tương tự : $\left\{ \begin{array}{l}I' \in B'C' \subset \left( {AB'C'} \right)\\I' \in \left( {AA'I'I} \right)\end{array} \right.$ $\Rightarrow I' \in \left( {AB'C'} \right) \cap \left( {AA'I'I} \right)$

⇒ (AB′C′) ∩ (AA′I′I) = AI′

Gọi AI′ ∩ A′I = E. Ta có:

$\left\{ \begin{array}{l}E \in A'I\\E \in AI' \subset \left( {AB'C'} \right)\end{array} \right.$ $\Rightarrow E = A'I \cap \left( {AB'C'} \right)$

Vậy E là giao điểm của A’I và mặt phẳng (AB’C’).

LG c

Tìm giao tuyến của $(AB’C’)$ và $(A’BC)$

Phương pháp giải:

Sử dụng tính chất nếu hai mặt phẳng $(\alpha)$ và $(\beta)$ có điểm chung $S$ và lần lượt chứa hai đường thẳng song song $d$ và $d’$ thì giao tuyến của $(\alpha)$ và $(\beta)$ là đường thẳng $\Delta$ đi qua $S$ và song song với $d$ và $d’$ .

Sử dụng tính chất của hình bình hành.

Sử dụng định lý Talet.

Lời giải chi tiết:

Trong (ABB’A’), gọi $A'B \cap AB' = M$ $\Rightarrow \left\{ \begin{array}{l}M \in A'B \subset \left( {A'BC} \right)\\M \in AB' \subset \left( {AB'C'} \right)\end{array} \right.$ $\Rightarrow M \in \left( {A'BC} \right) \cap \left( {AB'C'} \right)$

Trong (ACC’A’) gọi $A'C \cap AC' = N$ $\Rightarrow \left\{ \begin{array}{l}N \in A'C \subset \left( {A'BC} \right)\\N \in AC' \subset \left( {AB'C'} \right)\end{array} \right.$ $\Rightarrow N \in \left( {A'BC} \right) \cap \left( {AB'C'} \right)$

Vậy (AB′C′) ∩ (A′BC) = MN.

Cách lập luận khác:

Ta có $A’I\cap (AB’C’)=E$ mà $A’I\subset (A’BC)$ $\Rightarrow E\in (A’BC)\cap (AB’C’)$ .

Ta lại có $(A’BC), (AB’C’)$ lần lượt có hai đường thẳng $BC\parallel B’C’$

Suy ra $(A’BC)\cap (AB’C’)=Ex$ , $Ex\parallel BC\parallel B’C’$ .

Tứ giác $AA’I’I$ là hình bình hành có hai đường chéo là $A’I$ và $AI’$ giao nhau tại $E$ nên $E$ là trung điểm mỗi đường.

Suy ra $E$ là trung điểm của $A’I$

Tam giác $A’BC$ có $Ex\parallel BC$ và $E$ là trung điểm của $A’I$ nên $Ex\cap A’B=M, Ex\cap A’C=N$ khi đó $M$ là trung điểm của $A’B$ , $N$ là trung điểm của $A’C$ .

Tứ giác $A’ABB’$ và $A’ACC’$ là hình bình hành có $M$ $N$ lần lượt là trung điểm của đường chéo nên cũng là trung điểm của đường chéo còn lại.

Suy ra $MN\subset (AB’C’)$

Suy ra $(AB’C’)\cap (A’BC)=MN$ .

SBT Toán lớp 11