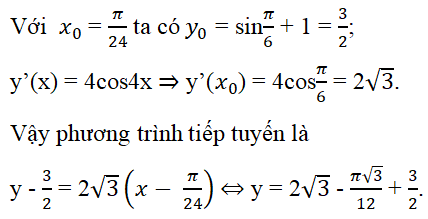Cho hàm số y = sin4x
LG a
Chứng minh rằng sin4(x + kπ/2) = sin4x với k ∈ Z.
Từ đó vẽ đồ thị của hàm số
y = sin4x; (C1)
y = sin4x + 1. (C2)
Lời giải chi tiết:
Ta có sin4(x + kπ/2) = sin(4x + k2π) = sin4x với k ∈ Z.
Từ đó suy ra hàm số y = sin4x là hàm số tuần hoàn với chu kì π/2.
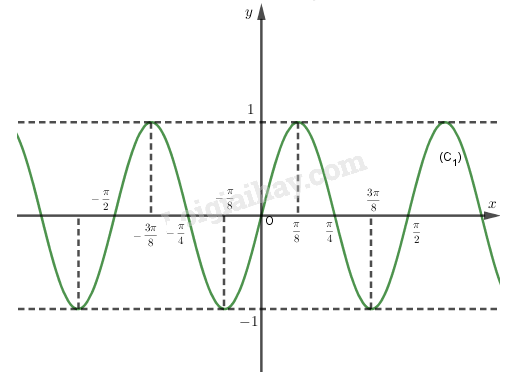
Vẽ đồ thị hàm số y = sin4x.
Xét trên một chu kì T=[0;π2] ta có:
Đồ thị hàm số y = sin4x đi qua các điểm (0;0),(π8;1),(π4;0), (3π8;−1),(π2;0)
Vì hàm số y = sin4x (C1) là hàm số lẻ nên đồ thị của nó có tâm đối xứng là gốc tọa độ O.
Ta có đồ thị như sau:
Đồ thị hàm số y = sin4x + 1 (C2) có được từ việ tịnh tiến đồ thị (C1) lên 1 đơn vị như sau:
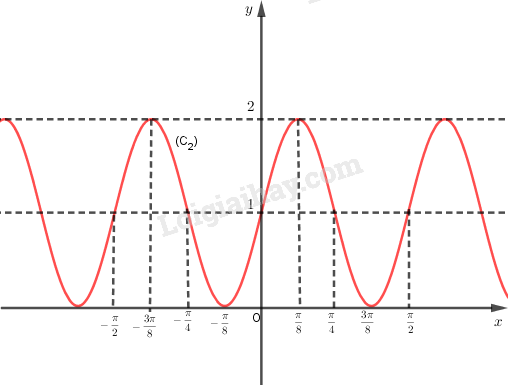
LG b
Xác định giá trị của m để phương trình: sin4x + 1 = m (1)
- Có nghiệm
- Vô nghiệm
Lời giải chi tiết:
Cách 1:
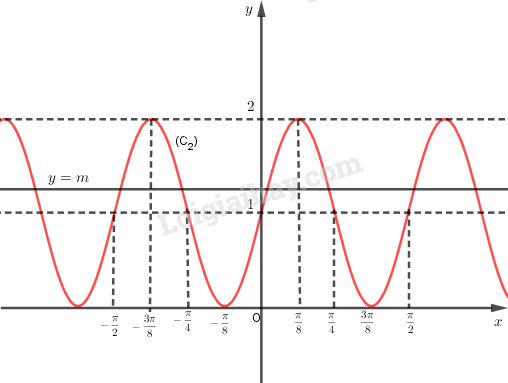
Số nghiệm của phương trình sin4x+1=m bằng số giao điểm của đồ thị (C2) với đường thẳng y=m.
Quan sát đồ thị ta thấy,
Phương trình có nghiệm khi 0≤m≤2.
Phương trình vô nghiệm khi m>2 hoặc m<0.
Cách 2:
Vì sin4x + 1 = m ⇔ sin4x = m – 1
Mà -1 ≤ sin4x ≤ 1 nên -1 ≤ m – 1 ≤ 1
⇔ 0 ≤ m ≤ 2.
Từ đó, phương trình (1) có nghiệm khi 0 ≤ m ≤ 2 và vô nghiệm khi m > 2 hoặc m < 0.
LG c
Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ x0 = π/24.
Lời giải chi tiết:
Phương trình tiếp tuyến của (C2) có dạng
y - yo = y’(xo)(x - xo).