Đề bài
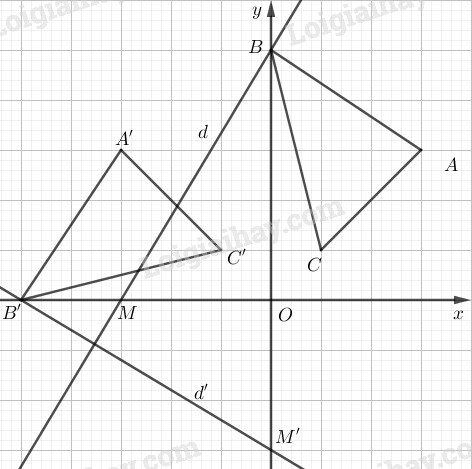
Trong mặt phẳng Oxy cho các điểm A(3;3), B(0;5), C(1;1) và đường thẳng d có phương trình 5x−3y+15=0. Hãy xác định tọa độ các đỉnh của tam giác A′B′C′ và phương trình của đường thẳng d′ theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90o.
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa:
Cho O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M′ sao cho OM′=OM và góc lượng giác (OM;OM′) bằng α được gọi là phép quay tâm O góc α.
Lời giải chi tiết
Gọi Q(O,90o) là phép quay tâm O, góc quay 90o.
Điểm A′(−3;3), B′(−5;0), C′(−1;1).
Đường thẳng d đi qua B và M(−3;0).
Ta có M′=Q(O,90o)(M)=(0;−3) nên d′ là đường thẳng B′M′.
→B′M′=(5;−3)⇒→nB′M′=(3;5) là VTPT của B'M'.
Mà B'M' đi qua B'(-5;0) nên B'M': 3(x+5)+5(y-0)=0 hay 3x+5y+15=0.
Vậy d' có phương trình 3x+5y+15=0.