Đề bài
Cho đường tròn \(\left( C \right)\) và hai điểm cố định phân biệt \(A,B\) thuộc \(\left( C \right)\). Với mỗi điểm \(M\) chạy trên đường tròn (trừ hai điểm \(A,B\)), ta xét điểm \(N\) sao cho \(AMBN\) là hình bình hành. Chứng minh rằng tập hợp các điểm \(N\) cũng nằm trên một đường tròn xác định.
Phương pháp giải - Xem chi tiết
Dựng hình và nhận xét
Lời giải chi tiết
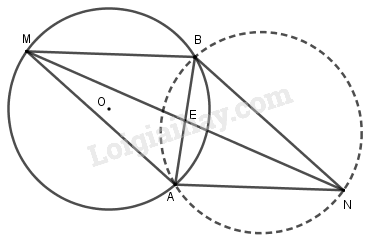
Gọi \(E = AB \cap MN\) thì \(E\) là trung điểm của \(AB,MN\).
Dễ thấy \(N = {D_E}\left( M \right)\) và \(M \in \left( C \right)\) nên tập hợp các điểm \(N\) thuộc đường tròn \(\left( {C'} \right)\) là ảnh của \(\left( C \right)\) qua phép đối xứng qua trung điểm của \(AB\).

