Đề bài
Cho hình chóp \(S.ABCD \) có đáy là hình thang \(ABCD \) (có đáy nhỏ \(BC\)). Gọi \(M, N\) lần lượt là trung điểm của \(AB \) và \(SD, O \) là giao điểm của \(AC \) và \(DM\).
a) Tìm giao điểm của \(MN\) và mặt phẳng \((SAC)\) .
b) Tìm thiết diện của hình chóp với mặt phẳng \((NBC)\). Thiết diện đó là hình gì?
Phương pháp giải - Xem chi tiết
a) Tìm mặt phẳng chứa \(MN\) và cắt \((SAC)\).
Tìm giao tuyến của \((SAC)\) với mặt phẳng vừa tìm.
Tìm giao điểm của \(MN\) với giao tuyến trên và kết luận.
b) Tìm giao tuyến của \((NBC)\) với các mặt của hình chóp (nếu có).
Lời giải chi tiết
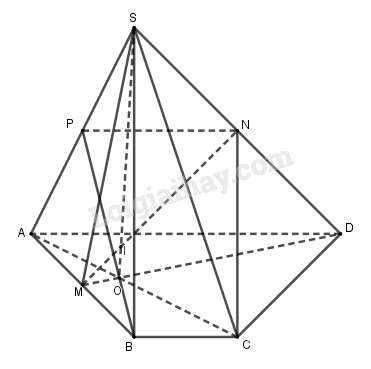
a) Gọi \(O = AC \cap MD\).
Ta có: \(\left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in MD \subset \left( {SMD} \right)\end{array} \right.\) \( \Rightarrow O \in \left( {SAC} \right) \cap \left( {SMD} \right)\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SMD} \right)\)
\( \Rightarrow SO = \left( {SAC} \right) \cap \left( {SMD} \right)\)
Trong mặt phẳng \((SMB) \) gọi \(I = SO \cap MN\).
Ta có:
\(\left\{ \begin{array}{l}
I \in MN\\
I \in SO \subset \left( {SAC} \right)
\end{array} \right. \)
\(\Rightarrow I = \left( {SAC} \right) \cap MN\)
b) \(A{\rm{D}}\parallel BC\left( {BC \subset \left( {SBC} \right)} \right)\)
\( \Rightarrow A{\rm{D}}\parallel \left( {SBC} \right)\).
Mặt phẳng \((SAD) \) cắt mặt phẳng \((NBC) \) theo giao tuyến \(NP\parallel A{\rm{D}}\left( {P \in SA} \right)\).
Ta có thiết diện cần tìm là hình thang \(BCNP\).

