Giải bài 2.22 trang 77 SBT hình học 11

130 lượt xem

Lựa chọn câu để xem lời giải nhanh hơn

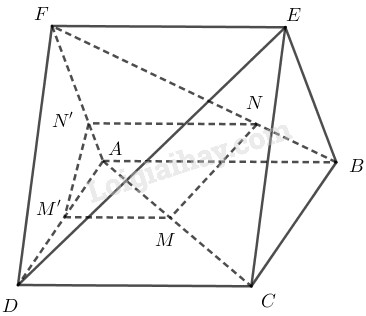
Cho hai hình vuông $ABCD$ và $ABEF$ ở trong hai mặt phẳng phân biệt. Trên các đường chéo $AC$ và $BF$ lần lượt lấy các điểm $M$ và $N$ sao cho $AM = BN$ . Các đường thẳng song song với $AB$ vẽ từ $M$ và $N$ lần lượt cắt $AD$ và $AF$ tại $M’$ và $N’$ . Chứng minh

LG a

$\left( {A{\rm{D}}F} \right)\parallel \left( {BCE} \right)$ .

Phương pháp giải:

Sử dụng tính chất: Nếu đường thẳng $d$ không nằm trong mặt phẳng $(\alpha)$ và $d$ song song với $d’$ nằm trong $(\alpha)$ thì $d$ song song với $(\alpha)$ .

$\left\{ \begin{array}{l}d \not\subset (\alpha )\\d\parallel d'\\d' \subset (\alpha )\end{array} \right. \Rightarrow d\parallel (\alpha )$

Sử dụng tính chất: Nếu mặt phẳng $(\alpha)$ chứa hai đường thẳng cắt nhau $a, b$ và hai đường thẳng này cùng song song với mặt phẳng $(\beta)$ thì mặt phẳng $(\alpha)$ song song với mặt phẳng $(\beta)$ .

$\left\{ \begin{array}{l}a \subset (\alpha ),b \subset (\alpha )\\a\text{ cắt }b\\a\parallel (\beta ),b\parallel (\beta )\end{array} \right. \Rightarrow (\alpha )\parallel (\beta )$

Lời giải chi tiết:

Ta có:

$\left\{ \begin{array}{l}AD\parallel BC\\BC \subset (BCE)\end{array} \right. \Rightarrow AD\parallel (BCE)$

$\left\{ \begin{array}{l}AF\parallel BE\\BE \subset (BCE)\end{array} \right. \Rightarrow AF\parallel (BCE)$

Mà $AD, AF\subset (ADF)$

Nên $(ADF)\parallel (BCE)$ .

LG b

$M'N'\parallel DF$ .

Phương pháp giải:

Sử dụng định lý Talet.

Lời giải chi tiết:

Vì $ABCD$ và $ABEF$ là các hình vuông nên $AC=BF$

Ta lại có $MM’\parallel CD\Rightarrow \dfrac{AM’}{AD}=\dfrac{AM}{AC}$

Và $NN’\parallel AB\Rightarrow \dfrac{AN’}{AF}=\dfrac{BN}{BF}$

Suy ra $\dfrac{AM’}{AD}=\dfrac{AN’}{AF}\Rightarrow M’N’\parallel DF$ .

LG c

$\left( {DEF} \right)\parallel \left( {MM'N'N} \right)$ và $MN\parallel \left( {DEF} \right)$

Phương pháp giải:

Sử dụng tính chất: Nếu đường thẳng $d$ không nằm trong mặt phẳng $(\alpha)$ và $d$ song song với $d’$ nằm trong $(\alpha)$ thì $d$ song song với $(\alpha)$ .

$\left\{ \begin{array}{l}d \not\subset (\alpha )\\d\parallel d'\\d' \subset (\alpha )\end{array} \right. \Rightarrow d\parallel (\alpha )$

$\left\{ \begin{array}{l}a \subset (\alpha ),b \subset (\alpha )\\a\text{ cắt }b\\a\parallel (\beta ),b\parallel (\beta )\end{array} \right. \Rightarrow (\alpha )\parallel (\beta )$

Sử dụng tính chất khi $(\alpha)$ song song với $(\beta)$ thì $(\alpha)$ sẽ song song với mọi đường thẳng thuộc $(\beta)$ .

Sử dụng tính chất khi $(\alpha)\parallel (\beta)$ thì $(\alpha)$ song song với mọi đường thuộc $(\beta)$ .

Lời giải chi tiết:

Vì $\left\{ \begin{array}{l}DF\parallel M'N'\\M'N' \subset (MM'N'N)\end{array} \right.$

$\Rightarrow DF\parallel (MM'N'N)$

$\left\{ \begin{array}{l}NN'\parallel AB \Rightarrow NN'\parallel {\rm{EF}}\\NN' \subset (MM'N'N)\end{array} \right.$

$\Rightarrow EF\parallel (MM'N'N)$

Mà $DF, EF\subset (DEF)$ nên $(DEF)\parallel (MM’N’N)$ .

Vì $(MM’N’N)\parallel (DEF)$ và $MN\subset (MM’N’N)$ suy ra $MN\parallel (DEF)$ .

SBT Toán lớp 11