Đề bài
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Gọi \(M\) và \(N\) là hai điểm di động tương ứng trên \(AD\) và \(BE\) sao cho \(\dfrac{AM}{MD} = \dfrac{BN}{NE}\)
Chứng minh rằng đường thẳng \(MN\) luôn luôn song song với một mặt phẳng cố định. Hãy chỉ ra mặt phẳng cố định đó.
Phương pháp giải - Xem chi tiết
Sử dụng định lý Talet.
Sử dụng tính chất: Nếu đường thẳng \(d\) không năm trong mặt phẳng \((\alpha)\) và \(d\) song song với đường thẳng \(d’\) nằm trong \((\alpha)\) thì \(d\) song song với \((\alpha)\).
\(\left\{ \begin{array}{l}d \not\subset (\alpha )\\d\parallel d'\\d' \subset (\alpha )\end{array} \right. \Rightarrow d\parallel (\alpha )\)
Sử dụng tính chất: Nếu mặt phẳng \((\alpha)\) chứa hai đường thẳng cắt nhau \(a\), \(b\) và hai đường thẳng này cùng song song với mặt phẳng \((\beta)\) thì \((\alpha)\) song song với \((\beta)\).
\(\left\{ \begin{array}{l}a \subset (\alpha ),b \subset (\alpha )\\a\text{ cắt }b\\a\parallel (\beta ),b\parallel (\beta )\end{array} \right. \Rightarrow (\alpha )\parallel (\beta )\)
Sử dụng tính chất khi \((\alpha)\) song song với \((\beta)\) thì \((\alpha)\) sẽ song song với mọi đường thẳng thuộc \((\beta)\).
Lời giải chi tiết
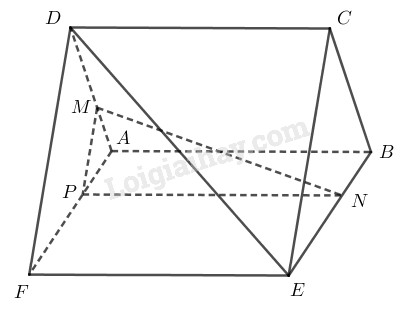
Trong hình bình hành \(ABEF\), ta dựng \(NP\parallel AB\parallel EF\).
Mà \(EF\subset (DEF)\)
\(\Rightarrow NP\parallel (DEF) \text{ (1)}\)
Từ các dựng \(NP\parallel AB\parallel EF\) suy ra \(\dfrac{BN}{NE}=\dfrac{AP}{PF}\).
Mà \(\dfrac{BN}{NE}=\dfrac{AM}{MD}\) \(\Rightarrow\dfrac{AP}{PF}=\dfrac{AM}{MD}\)
Suy ra \(PM\parallel FD\) mà \(FD\subset (DEF)\)
\(\Rightarrow PM\parallel (DEF) \text{ (2)}\)
Ta lại có \(NP, MP\subset (MNP)\), từ \(\text{(1)}\) và \(\text{(2)}\) suy ra \((MNP)\parallel(DEF)\).
Ta có: \(MN\subset(MNP)\Rightarrow MN\parallel (DEF)\)
Vậy \(MN\) luôn song song với một mặt phẳng cố định \((DEF)\).

