Đề bài
Cho tứ diện \(ABCD\). Tìm vị trí điểm \(M\) trong không gian sao cho: \(M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị cực tiểu.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất:
Cho \(I\) là trung điểm đoạn thẳng \(AB\). Với điểm \(M\) bất kì ta luôn có:
\(MA^2+MB^2=2MI^2+\dfrac{1}{2}AB^2\)
Lời giải chi tiết
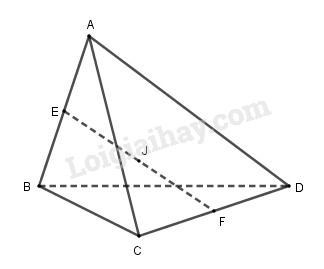
Gọi \(\displaystyle E, F\) lần lượt là trung điểm của \(\displaystyle AB\) và \(\displaystyle CD\). Ta có:
\(\begin{array}{l}
M{A^2} + M{B^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2}\\
= {\left( {\overrightarrow {ME} + \overrightarrow {EA} } \right)^2} + {\left( {\overrightarrow {ME} + \overrightarrow {EB} } \right)^2}\\
= {\overrightarrow {ME} ^2} + 2\overrightarrow {ME} .\overrightarrow {EA} + {\overrightarrow {EA} ^2}\\
+ {\overrightarrow {ME} ^2} + 2\overrightarrow {ME} .\overrightarrow {EB} + {\overrightarrow {EB} ^2}\\
= 2M{E^2} + 2\overrightarrow {ME} \left( {\overrightarrow {EA} + \overrightarrow {EB} } \right) + E{A^2} + E{B^2}\\
= 2M{E^2} + 0 + \frac{1}{4}A{B^2} + \frac{1}{4}A{B^2}\\
= 2M{E^2} + \frac{1}{2}A{B^2}
\end{array}\)
Do đó, \(\displaystyle M{A^2} + M{B^2} = 2M{E^2} + {1 \over 2}A{B^2}\,\,\,\,\,\left( 1 \right)\)
\(\displaystyle M{C^2} + M{D^2} = 2M{F^2} + {1 \over 2}C{{\rm{D}}^2}\,\,\,\,\,\left( 2 \right)\)
Cộng (1) và (2) ta có:
\(\displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\)
\(\displaystyle = 2\left( {M{E^2} + M{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}\,\,} \right)\,\,\)
Gọi \(\displaystyle J\) là trung điểm của \(\displaystyle EF\), ta có:
\(\displaystyle \left( {M{E^2} + M{F^2}} \right) = 2M{J^2}\, + {1 \over 2}E{F^2}\)
Khi đó:
\(\displaystyle \eqalign{
& M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2} \cr
& = 2\left( {2M{J^2}\, + {1 \over 2}E{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr
& = 4M{J^2} + E{F^2} + \frac{1}{2}\left( {A{B^2} + C{D^2}} \right)\cr &\ge E{F^2} + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr} \)
Vậy \(\displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị nhỏ nhất khi \(MJ = 0\) hay \(\displaystyle M \equiv J\).
