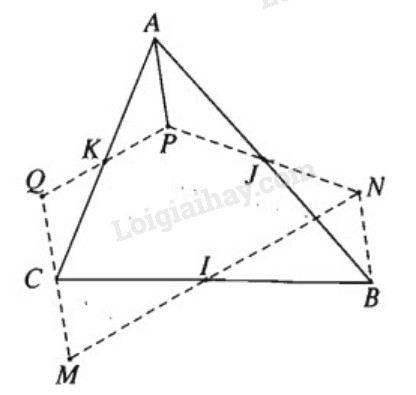
Đề bài
Cho ba điểm không thẳng hàng I, J, K. Hãy dựng tam giác ABC nhận I, J, K lần lượt là trung điểm của các cạnh BC, AB, AC.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất tâm đối xứng bảo toàn khoảng cách giữa hai điểm.
Lời giải chi tiết
Giả sử tam giác ABC đã dựng được.
Cách dựng điểm C:
Lấy điểm M bất kì. Gọi N là ảnh của M qua phép đối xứng tâm I. P là ảnh của N qua phép đối xứng tâm J. Q là ảnh của P qua phép đối xứng tâm K.
Khi đó →CM=−→BN=→AP=−→CQ.
Do đó C là trung điểm của QM.
Tương tự, cách dựng điểm B:
Lấy điểm O bất kỳ, gọi O1 là ảnh của O qua phép đối xứng tâm J, O2 là ảnh của O1 qua phép đối xứng tâm K, O3 là ảnh của O2 qua phép đối xứng tâm I
B là trung điểm của OO3.
Cách dựng điểm A:
Lấy điểm H bất kỳ, gọi H1 là ảnh của H qua phép đối xứng tâm J, H2 là ảnh của H1 qua phép đối xứng tâm K, H3 là ảnh của H2 qua phép đối xứng tâm I
A là trung điểm của HH3.
Từ đó suy ra cách dựng tam giác ABC.