Đề bài
Cho tứ diện SABC có SA, SB, SC vuông góc với nhau từng đôi một. Gọi H là hình chiếu vuông góc của S lên mp(ABC).
a) Chứng minh rằng H là trực tâm của tam giác ABC.
b) Chứng minh rằng \(\dfrac{1}{{S{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{S{B^2}}} + \dfrac{1}{{S{C^2}}}\)
c) Chứng minh rằng (SSBC)2 = (SHBC). (SABC) và
(SABC)2 = (SSAB)2 + (SSBC)2 + (SSCA)2
d) Chứng minh rằng
SG2 = (SA2 + SB2 + SC2)/9 (G là trọng tâm của tam giác ABC) và
(AB + BC + CA)2 ≤ 6(SA2 + SB2 + SC2).
e) Chứng minh rằng tam giác ABC có ba góc nhọn và
SA2tanA = SB2tanB = SC2tanC = 2SABC
Lời giải chi tiết
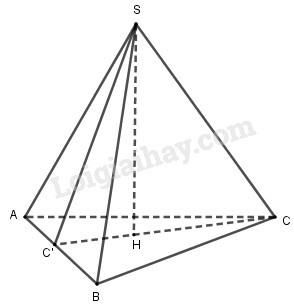
a) Ta chứng minh: CH ⊥ AB & AH ⊥ BC
Ta có: AB ⊥ SC (do SH ⊥ (ABC)) & AB ⊥ SH (do SC ⊥ (SAB))
⇒ AB ⊥ (SCH) ⇒ AB ⊥ CH (1)
Tương tự, ta có BC ⊥ (SAH) nên AH ⊥ BC (2)
Từ (1) và (2) cho ta H là trực tâm ΔABC.
b) Giả sử CH kéo dài cắt AB tại C’, ta có
AB ⊥ CC' (do H là trực tâm) & AB ⊥ SC' (do AB ⊥ (SCH))
Trong tam giác SCC’, ta có \(\dfrac{1}{{S{H^2}}} = \dfrac{1}{{S{C^2}}} + \dfrac{1}{{SC{'^2}}}\) (3)
Mà SC’ là đường cao trong tam giác vuông SAB nên
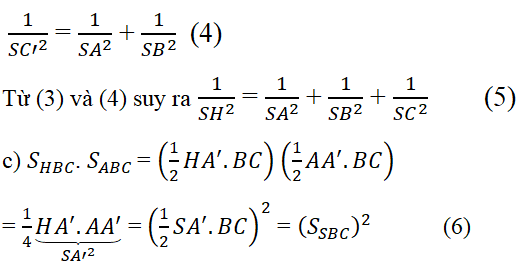
Tương tự, ta có (SSCA )2 = SHCA. SABC (7)
(SSAB )2 = SHAB. SABC (8)
Cộng (6), (7), (8) vế theo vế, ta có
\(\begin{array}{l}{\left( {{S_{SBC}}} \right)^2} + {\left( {{S_{SCA}}} \right)^2} + {\left( {{S_{SAB}}} \right)^2}\\ = {S_{ABC}}\left( {{S_{HBC}} + {S_{HCA}} + {S_{HAB}}} \right)\\ = {S_{ABC}}.{S_{ABC}} = {\left( {{S_{ABC}}} \right)^2}\end{array}\)

Áp dụng bất đẳng thức Cô-si, ta có:
2AB. BC ≤ AB2 + BC2
2CA. AB ≤ CA2 + AB2
2BC. CA ≤ BC2 + CA2
Suy ra (AB + BC + CA)2 = AB2 + BC2 + CA2 + 2(AB.BC + BC.CA + CA.AB)
≤ 3(AB2 + BC2 + CA2)
≤ 3(SA2 + SB2 + SB2 + SC2 + SC2 + SA2)
≤ 6(SA2 + SB2 + SC2).
e) Đặt SA = a, SB = b, SC = c
Trong ΔABC, ta có: \(\cos A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}}\) \( = \dfrac{{{a^2}}}{{\sqrt {\left( {{a^2} + {b^2}} \right)\left( {{a^2} + {c^2}} \right)} > 0}}\)
Tương tự cosB > 0, cosC > 0.
Vậy ΔABC có ba góc nhọn.
Mặt khác, ta có:
\(\begin{array}{l}S{A^4}.{\tan ^2}A = {a^4}\left( {\dfrac{1}{{{{\cos }^2}A}} - 1} \right)\\ = {a^4}\left[ {\dfrac{{\left( {{a^2} + {b^2}} \right)\left( {{a^2} + {c^2}} \right)}}{{{a^4}}} - 1} \right]\end{array}\)
= (a2 + b2)(a2 + c2) - a4 = a2 b2 + b2 c2 + c2 a2
= 4(SSAB2 + SSBC2 + SSCA2) = 4(SABC)2
⇒ SA2tanA = 2SABC.
Tương tự, ta có: SB2tanB = SC2tanC = 2SABC.
Vậy SA2tanA = SB2tanB = SC2tanC = 2SABC.

