Đề bài
Cho hình hộp \(ABCD.A’B’C’D’\) có \(P\) và \(R\) lần lượt là trung điểm các cạnh \(AB\) và \(A’D’\). Gọi \(P’, Q, Q’,R'\) lần lượt là tâm đối xứng của các hình bình hành \(ABCD, CDD’C’\), \(A’B’C’D’, ADD’A’\)
a) Chứng minh rằng \(\overrightarrow {PP'} + \overrightarrow {QQ'} + \overrightarrow {R{\rm{R}}'} = \overrightarrow 0 \)
b) Chứng minh hai tam giác \(PQR\) và \(P’Q’R’ \) có trọng tâm trùng nhau.
Phương pháp giải - Xem chi tiết
a) Biểu diễn các véc tơ trong biểu thức cần chứng minh về các véc tơ cơ sở của hình hộp và tính toán.
b) Sử dụng kết quả câu a, chú ý gọi \(G,G'\) là các trọng tâm rồi chứng minh \(G\) trùng \(G'\) hay \(\overrightarrow {GG'} = \overrightarrow 0\).
Lời giải chi tiết
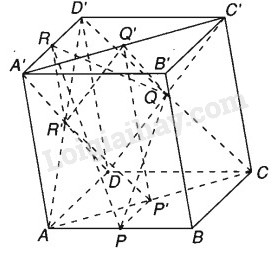
a) Ta có :\(\overrightarrow {PP'} = {1 \over 2}\overrightarrow {A{\rm{D}}} ,\overrightarrow {QQ'} = {1 \over 2}\overrightarrow {DA'} ,\) \(\overrightarrow {R{\rm{R}}'} = {1 \over 2}\overrightarrow {A'A} \)
Vậy: \(\overrightarrow {PP'} + \overrightarrow {QQ'} + \overrightarrow {R{\rm{R}}'}\) \( = {1 \over 2}\left( {\overrightarrow {A{\rm{D}}} + \overrightarrow {DA'} + \overrightarrow {A'A} } \right) = \overrightarrow 0 \)
b) Gọi \(G\) và \(G’ \) lần lượt là trọng tâm các tam giác \(PQR\) và \(P’Q’R’\).
Theo câu a) ta có: \(\overrightarrow {PP'} + \overrightarrow {QQ'} + \overrightarrow {R{\rm{R}}'} = \overrightarrow 0 \)
Do đó:
\(\left( {\overrightarrow {PG} + \overrightarrow {GG'} + \overrightarrow {G'P'} } \right) \) \(+ \left( {\overrightarrow {QG} + \overrightarrow {GG'} + \overrightarrow {G'Q'} } \right) \) \(+ \left( {\overrightarrow {RG} + \overrightarrow {GG'} + \overrightarrow {G'R'} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \underbrace {\left( {\overrightarrow {PG} + \overrightarrow {QG} + \overrightarrow {RG} } \right)}_{\overrightarrow 0 } + 3\overrightarrow {GG'} \) \( + \underbrace {\left( {\overrightarrow {G'P'} + \overrightarrow {G'Q'} + \overrightarrow {G'R'} } \right)}_{\overrightarrow 0 } = \overrightarrow 0 \)
\(3\overrightarrow {GG'} = \overrightarrow 0 \) ⟹\(G\) trùng với \(G’\)
Vậy hai tam giác \(PQR \) và \(P’Q’R’\) có cùng trọng tâm.

