Đề bài
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc và các cạnh OA = OB = OC = a, gọi I là trung điểm BC.
a) Chứng minh rằng: BC ⊥ (AOI), (OAI) ⊥ (ABC).
b) Tính góc giữa AB và mặt phẳng (AOI).
c) Tính góc giữa các đường thẳng AI và OB.
Lời giải chi tiết
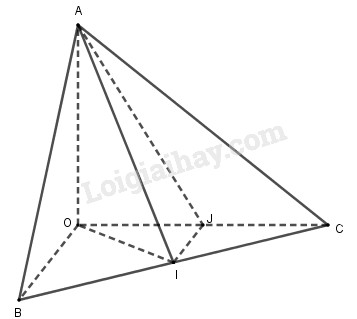
a) Ta có: \(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right.\) \( \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC\)
Mà \(\Delta OBC\) vuông cân tại O nên \(OI \bot BC\)
Do đó \(\left\{ \begin{array}{l}BC \bot OA\\BC \bot OI\end{array} \right. \Rightarrow BC \bot \left( {OAI} \right)\).
Mà \(BC \subset \left( {ABC} \right)\) nên \(\left( {ABC} \right) \bot \left( {OAI} \right)\).
b) Ta có: \(\left\{ \begin{array}{l}BI \bot OI\\BI \bot OA\end{array} \right. \Rightarrow BI \bot \left( {OAI} \right)\)
\( \Rightarrow I\) là hình chiếu của B trên \(\left( {OAI} \right)\).
Mà \(BA \cap \left( {OAI} \right) = A\) nên \(AI\) là hình chiếu của \(AB\) trên \(\left( {OAI} \right)\).
Do đó góc giữa AB và (OAI) bằng góc giữa AB và AI hay là góc \(\widehat {BAI}\).
Tam giác ABC có: \(AB = BC = AC\) do các tam giác vuông cân OAB,OAC,OBC bằng nhau.
Do đó ABC là tam giác đều nên \(\widehat A = {60^0}\)
I là trung điểm BC nên AI là phân giác góc A nên \(\widehat {BAI} = \dfrac{1}{2}\widehat A = {30^0}\).
c) Gọi J là trung điểm OC, khi đó IJ//OB
Do \(OB \bot \left( {OAC} \right)\) nên \(IJ \bot \left( {OAC} \right) \Rightarrow IJ \bot AJ\) hay tam giác \(AIJ\) vuông tại J.
Vậy góc giữa AI và OB bằng góc giữa AI và IJ hay góc \(\widehat {AIJ}\).
Có \(IJ = \dfrac{1}{2}OB = \dfrac{a}{2}\).
\(AJ = \sqrt {O{A^2} + O{J^2}} \) \( = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2}\).
Tam giác AIJ vuông tại J nên \(\tan \widehat {AIJ} = \dfrac{{AJ}}{{IJ}} = \dfrac{{a\sqrt 5 }}{2}:\dfrac{a}{2} = \sqrt 5 \) \( \Rightarrow \widehat {AIJ} = {65^0}54'\)

