Đề bài
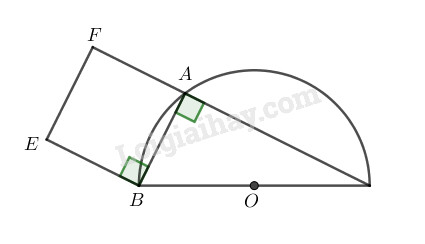
Cho nửa đường tròn tâm O đường kính BC. Điểm A chạy trên nửa đường tròn đó. Dựng về phía ngoài của tam giác ABC hình vuông ABEF. Chứng minh rằng E chạy trên một nửa đường tròn cố định.
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa:
Cho O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M′ sao cho OM′=OM và góc lượng giác (OM;OM′) bằng α được gọi là phép quay tâm O góc α.
Sử dụng tính chất phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
Lời giải chi tiết
Xem E là ảnh của A qua phép quay
tâm B, góc 90o. Khi A chạy trên nửa đường tròn (O), E sẽ chạy trên nửa đường tròn (O′) là ảnh của nửa đường tròn (O) qua phép quay tâm B, góc 90o.